(Click here for explanation in English.)

DSMC法の特徴の一つは，物理空間をセルと呼ばれる微細な空間要素に分割し，同一のセルに存在する分子同士で分子間衝突の計算を実行するというものである．そのため，セルを非常に小さくする必要があり，理想的には，セル一辺は平均自由行程以下にせねばならない（計算対象によっては平均自由行程の1/3以下が必要との報告もある）．密度が非常に低い宇宙空間なら，この条件は大して問題にはならないであろうが，それが例えば大気圧状態であるなら，平均自由行程は約0.066 $\mu$mとなり，1mmの長さには15000個のセルが必要で，1mm$^{2}$の面積なら2.3×10$^{8}$個となる．分子数としては，さらにその数倍が必要になるので，小型のPCでは扱えないし，計算時間も膨大なものになる．もちろん，セルを平均自由行程より大きくとって計算してもその結果が全く使い物にならないというわけではないが，厳密さに欠けるものになるのは避けられない．
私が大学の講義で平衡状態の分子速度の分布関数（マクスウェル分布）を解説しているとき，このマクスウェル分布をうまく利用してセルを大きくできないだろうかと考えたのが，このU_system を考案するきっかけである．DSMC法の通常の分子間衝突では，同じセルにある分子は，セル内で別々の位置にあるにもかかわらず，全て，同じ位置（例えばセル中心）にあると考えて衝突計算にかける．セルが平均自由行程を超えて大きくなるほど，セル内で遠く離れた位置にあって本来衝突するはずのない分子が衝突計算され，結果にひずみを作ることになる．そこで，もし，二つの分子を衝突させる際，元に位置に応じて分子の速度成分に修正を加えたらどうだろうか．その際，平衡状態の分布関数を利用できないだろうか．これが，U_systemの根底にある考え方です．
以下ではU_systemの説明をするにあたって，U_system用の例題プログラムを使用するが，これは，5.1節で解説したDSMC法の基礎プログラムにU_system部分を追加したものである．したがって，あらかじめ5.1節とそれに付属する基礎プログラムを十分に理解している必要がある．U_systemの説明中，例題プログラムの「〇行～〇行参照」のように表記するが，5.1節で行ったような丁寧な説明でなく，大雑把なものに留めており，また，必ずしも解説上の変数記号とFortranプログラムの変数記号が一致しているとは限らないので，細心の注意を払って読んでほしい．なお，U_systemコードについては，今回の軸対称流れ場の超音速噴流以外に，一次元垂直衝撃波に関するものが参考文献(9)の電子付録に掲載されているのでそれも参考にしてほしい．
　先に述べたように，従来の衝突計算法では，セルが大きくなるとそれに比例して二つの衝突分子の位置は離れるため，シミュレーションが忠実に行われなくなる．本来，衝突する2つの分子は同じ位置で選ばれるのが最も好ましいが，有限個の分子しか用いないシミュレーションでは，たとえセルを小さくしたとしても全く同じ位置で2つの分子を見つけるのは困難である．
　U_systemでは，衝突計算直前に一方の分子Pを，あたかも，もう一方の分子Qの位置に一致させたかのように分子速度の補正を行う．いま，流れ場中の分子は，全て，ある温度と流れ速度を持つ局所平衡状態の速度分布関数（マクスウェル分布）に従うものと仮定する．なお，以下では，2つの分子位置における速度分布関数をマクスウェル分布で仮定して補正式を導いているが，得られた補正式自体は，2つの位置の分布関数が必ずしもマクスウェル分布でなくとも有効である（例えば，マクスウェル分布式に現れる指数関数が別の関数に変わってもよい）．唯一必要な条件は，「分布中心が，流速に応じて左右に平行移動し，分子の熱運動速度が，温度の平方根に比例するような分布形状」というものである．大きいセルといっても同じセル内にある2つの分子であるから，マクスウェル分布でないとしても，上記の条件を満たすのはそれほど困難なことではない．
　さて，分子Ｐの位置の分布関数を$f_1$，分子Ｑの位置の分布関数を$f_2$とし，分子Pの速度が$f_1$上の一点Aにあるものとしよう（Fig.1）．

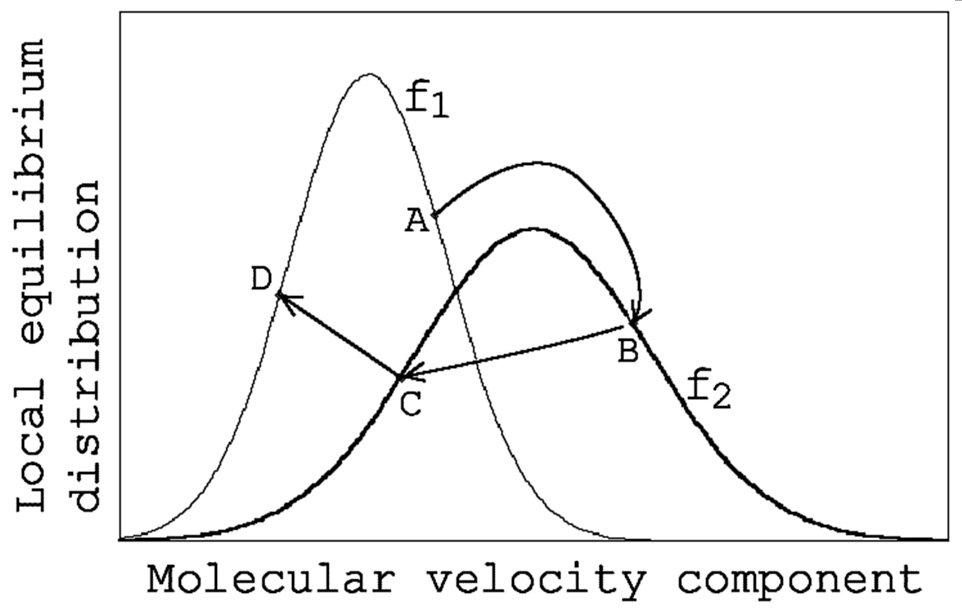
衝突計算に際して，このA点を分布関数$f_2$上のどこかに移せばよいことになるが，私が最も自然であると考えた方法は，$f_1$上のA点位置と$f_2$上の位置が相対的に同じになるよう移動させることである（B点）．このB点位置を求める計算は簡単である．いま，$x$方向速度成分$u$の分布関数について考えると，$f_1$と$f_2$は，次に示す式(1)および式(2)のように書ける．ここで，$R$は気体定数，$T_{x1}$, $T_{x2}$は，分子の並進運動に基づく温度3成分のうちの$x$方向速度成分により定義される温度（以下，$x$方向温度と呼ぶ）で，$U_1$，$U_2$は，流速の$x$成分である．

\begin{equation}
f_{1}=\frac{1}{\sqrt{2\pi R T_{x1}}}\exp\{-\frac{(u_{A}-U_{1})^2}{2 R T_{x1}}\}
\end{equation}

\begin{equation}
f_{2}=\frac{1}{\sqrt{2\pi R T_{x2}}}\exp\{-\frac{(u_{B}-U_{2})^2}{2 R T_{x2}}\}
\end{equation}

$f_1$および$f_2$をそれぞれ最大値で無次元化し，それらを等しいとおくと，次式となる．

\begin{equation}
\frac{(u_{A}-U_{1})^2}{T_{x1}}=\frac{(u_{B}-U_{2})^2}{T_{x2}}
\end{equation}

したがって，次式が得られる．

\begin{equation}
u_{B}=U_{2}+(u_{A}-U_{1})\sqrt{\frac{T_{x2}}{T_{x1}}}
\end{equation}

この修正された速度$u_B$（なお$u_A$は修正前の速度）を用いて，これ以降の計算は一般的な衝突計算法（Birdの計算法）で行う．結果として得られた衝突後の速度$u_C$ (C点) は，分子Pを元の位置に戻すのに伴い，次式を用いて再び修正される(D点)．

\begin{equation}
u_{D}=U_{1}+(u_{C}-U_{2})\sqrt{\frac{T_{x1}}{T_{x2}}}
\end{equation}

$v$ や $w$ も同様に修正されるが，二次元問題（軸対称問題）では，温度は$T_x$と$T_{yz}$しか使わず（$T_{yz}$の代わりに $T_y$ と$T_z$を使う方法もある），流速$w$ の修正に$W$は使われない．一次元問題では，温度 $T_x$と$T_{yz}$ を使うが，流速$v$と$w$の修正に $V$と$W$は使われない．なお，U_systemという名称であるが，上記のように見掛け上，衝突ペアのうちの片方の分子は，一旦，衝突相手の分子位置に移動し，衝突後に元の位置に戻ることになるので，Uターンするという意味でUを用い，また，この操作をすべての衝突ペアに対して実行する仕組み全体をsystemと表現して，このように名付けている．なお，セル内で流速と温度に変化がなければ，一般的な衝突計算法と同じものになる．
　ここで，式(4)(5)を用いるためには，分子PとQそれぞれの位置における流速$U$と温度$T$のデータが必要である．セルの端のデータが分かっているとして，一次元問題では単なる線形補間を使い，二次元問題では双線形補間を，三次元問題では三線形補間を使って求めることになる．なお，セル端のデータは，隣合うセル中心の値から導く．例題プログラムは軸対称問題であり，セルの４隅の値を用いた双線形補間となるので下記にその計算式を示す．

＜双線形補間＞ 二次元問題（軸対称問題）におけるセル内の任意位置の流速と温度の求め方：
長方形セルの四隅の座標を ($x$, $y$), ($x+A$, $y$), ($x$, $y+B$), ($x+A$, $y+B$) とし，その点の温度を $T_1$, $T_2$, $T_3$, $T_4$ とすると， セル内の任意位置 ($x+a$, $y+b$) における温度は，

\begin{equation}
T=(1－b/B)\{(1－a/A) T_{1}+ (a/A) T_{2}\} + (b/B)\{(1－a/A) T_{3} + (a/A) T_{4}\}
\end{equation}

で求められる．流速についても同様である．ところで，この双線形補間について，厳密ではないが簡単に体験する方法がある．日本料理で巻きずしを作るための調理器具に「巻きす」というものがあり，大きな百円ショップなら110円で手に入る．これをまず両手でピンと張って正方形の平面を作り，その後，両手を適当にひねると任意の滑らかな曲面が作られる．巻きすは，直線の竹ひごをひもで編んで作られているので，基本は線形であるが，滑らかな曲面を得ることができるのである．なお，三次元問題に適用する場合のセル８隅データを用いた三線形補間の計算式は少し複雑になるが，練習として読者諸君が導くとよい．

さて，最初の計算だけは，従来のDSMC法（Bird法）によって各セルの流速と温度を求める．DSMC法の長い繰返し計算の中で，従来の方法による計算は最初の１回だけでよく，以降は，U_systemによって流速と温度のデータが逐次更新される．なお，U_systemの計算１回に要する時間は，従来の計算法より増加するが，セルを大きくできる点を考慮すれば，計算全体での時間比較ではU_systemが有利となる．
　ところで，分子速度の補正を行うと，各衝突分子ペアの持つ運動量とエネルギが衝突前後で厳密には保存されない．もちろん流れ場全体としてあるいは長時間にわたって平均をとれば，統計的ばらつきの範囲内で保存される．しかし，多くの計算例を検討した結果，一回の衝突において，衝突前後のエネルギに大きな差が生じると，特に，数個のセル範囲で衝撃波が生じるような変化の激しい流れ場では，結果にひずみを成長させる原因となることが判明した．そこで，衝突前後でエネルギが保存されるような改良を加えたところ，U_systemの計算安定化は大きく改善された(U_system-3)．しかし，運動量に関する保存が保証されてないとの指摘があり，また，計算条件によっては温度上昇が予想外に生じるといった事例も発生して，更なる改善が望まれていた．Sunら（参考文献7）は，分子間衝突を無次元速度空間で行うことを考え，速度を無次元化するためのスケール変数に流速と温度を用いるという概念を導入してDSMC解析を行っている（LCDSMC法）．その計算法は，基本的には，私の提案したU_systemと同じ算法ではあるが，特筆すべきは，分子の運動量と並進エネルギを各セルごとに厳密保存するために，Pareschiら（参考文献8）が提案した補正方法を採用したことである．次に，その方法を説明する．
ある流速と温度が与えられた局所平衡状態の速度分布関数から，乱数を用いて，多数の分子の速度を再現した場合，再現された分子の速度から，逆に流速と温度を求めても，厳密には元に戻らない．これを厳密に元に戻すために，Pareschiらは，運動量とエネルギの厳密保存の方法を考案した．いま，この方法をU_systemに適用することを考える．衝突前と衝突後の分子速度成分を$u$, $v$, $w$および$u^{*}$, $v^{*}$, $w^{*}$ とし，これを，Pareschiらの補正法を使って運動量とエネルギを厳密保存して最終的に $u^{+}$, $v^{+}$, $w^{+}$ となるものとしよう．この場合，補正は式(7)のように，4つのパラメータ $\lambda_X$, $\lambda_Y$, $\lambda_Z$, $\tau$ によって行うことになる．（注意）5.1節において平均自由時間として使われた$\tau$と同じ記号が用いられているが，これはPareschiらの原論文に倣ったもので，混同しないよう注意してほしい．なお，Fortranプログラムの変数記号としては，平均自由時間は TAU，補正パラメータの方は ATAU として区別している．

\begin{equation}
u^{+}=(u^{*}-\lambda_{X})/\tau, 　　

v^{+}=(v^{*}-\lambda_{Y})/\tau, 　　

w^{+}=(w^{*}-\lambda_{Z})/\tau
\end{equation}

ここで， $\lambda_X$, $\lambda_Y$, $\lambda_Z$, $\tau$ を求めるために，次式(8)~(11)に示す運動量保存式とエネルギ保存式を用いる．なお，$m$は分子質量，添え字 $i$ は，全ての分子について和を求めることを意味する．

\begin{equation}
\sum m_i (u^*_i – \lambda_X)/\tau =\sum m_i u_i
\end{equation}

\begin{equation}
\sum m_i (v^*_i – \lambda_Y)/\tau =\sum m_i v_i
\end{equation}

\begin{equation}
\sum m_i (w^*_i – \lambda_Z)/\tau =\sum m_i w_i
\end{equation}

\begin{equation}
\sum m_i [ \{(u^*_i-\lambda_X)/\tau\}^2 +\{(v^*_i-\lambda_Y)/\tau\}^2 +\{(w^*_i-\lambda_Z)/\tau\}^2 ] = \sum m_i(u^2_i+v^2_i+w^2_i)
\end{equation}
結果として，$\tau$, $\lambda_X$, $\lambda_Y$, $\lambda_Z$ は下記の一連の式で求められる．

\begin{equation}
\tau = \pm \sqrt{[\sum m_i \sum \{ m_i ( u^{*2}_i + v^{*2}_i + w^{*2}_i ) \}\ – A^*] \ / \ [\sum m_i \sum \{ m_i ( u^{2}_i + v^{2}_i + w^{2}_i ) \}\ – A]}
\end{equation}
\begin{equation}
A^* = (\sum m_i u^*_i)^2 +(\sum m_i v^*_i)^2 +(\sum m_i w^*_i)^2
\end{equation} \begin{equation}
A = (\sum{m_i u_i})^2 +(\sum{m_i v_i})^2 +(\sum{m_i w_i})^2
\end{equation}

　

\begin{equation}
\lambda_X = (\sum{m_i u^*_i} – \ \tau \sum{m_i u_i}) / \sum m_i
\end{equation}

\begin{equation}
\lambda_Y = (\sum{m_i v^*_i} – \ \tau \sum{m_i v_i}) / \sum m_i
\end{equation}

\begin{equation}
\lambda_Z= (\sum{m_i w^*_i} – \ \tau \sum{m_i w_i}) / \sum m_i
\end{equation}

　

本ブログに収められたU_systemは，上記に示した運動量とエネルギの厳密保存を施したものである．なお，$\tau$ を求める際に，平方根の前の符号には必ず正を用いる必要がある．負であっても保存則は満足するが，負であると，補正前後の速度方向を一致させるために，修正用パラメータ $\lambda_X$, $\lambda_Y$, $\lambda_Z$ が非常に大きな値になってしまう（補正値 $\lambda_X$, $\lambda_Y$, $\lambda_Z$ と流速の絶対値がほぼ同じ大きさになる）．一方，正の場合，$\lambda_X$, $\lambda_Y$, $\lambda_Z$ は流速の1/100以下である．もともと式(7)は修正に使うものであり，修正前後で差異が小さいことを想定しているので，差異の小さい方を採用する．実際に適用した結果でも，平方根の前の符号に負を用いると，保存則は成立するがU_systemの効果は殆どなくなってしまう．ちなみに，このPareschiらの厳密保存の方法は，南部法(修正南部法)（参考文献20）に適用すれば南部法の欠点を補えるのではないかとも考えられる．

＜課題＞
DSMC法の難易度は，３次元，軸対称，２次元，１次元と低くなってくるが，一番容易なのは，ゼロ次元問題である．ゼロ次元問題は，物理空間が一様なので，セルは１個で良く，セルに多数の分子を入れることができるので，分子数の大小の影響を調べるのにも使われる．参考文献(11)の最後に書かれているDSMC法を用いた平均自由行程の計算はゼロ次元問題の一例である．さて，このゼロ次元問題として，Pareschiらの運動量とエネルギの厳密保存の効果を調査してみよう．初期状態として，ある温度と流速（例えば，T=288K, U=10m/s, V=0, W=0）で局所平衡状態にあるアルゴン単一気体を考えることにする．まず，その初期条件から乱数を使って分子を１万個発生させ，その１万個の分子情報から温度と流速がどうなったか調べてみる（流速については音速を基準に変動が生ずるのであまり問題視せず，ここでは特に「温度の変動」に着目して眺めてほしい）．当然，初期状態とほとんど同じ値になっているはずであるが，１万個しか使っていないので状態はわずかに変化して，初期状態と完全には一致しない．そして次に，その得られた温度と流速を使って，再び分子を１万個発生させ，温度と流速がどのようになるかを調べ，これを何度も繰り返してみる．一見すると，毎回毎回の温度（と流速）は多少の変動はしても，初期状態から大きくずれることはないように思われる．しかし，残念ながら，そうはならず，１万個の分子発生を３万回も続けていくと，とんでもない結果が待ち受けている．そう，乱歩という現象が生じているのである．一方，毎回の１万個分子発生の直後に，Pareschiらの補正を行ってみたら結果はどうなるであろうか．．．．． この計算は，練習問題として読者諸君にぜひ挑戦してもらいたい．なお，無料のFortranコンパイラはネットで手に入れることができるし，他の言語で挑戦してもらってもよい．計算速度を気にしないのなら，エクセルに付属するインタープリタ方式の VBA言語（これは文法がFortranに非常に近い．．．というか，VBAの元となっているBasic言語はFortranをまねてPC用に作られたので当然ではある．50年前の技術計算用言語はFortranしかなかった）を使ってみてもよい．

　

Fortranプログラム USYS2024-3NEG.F（ここをクリックするとそのプログラムに飛ぶ）は，元の基礎プログラム（5.1節参照）に U_system 部分を追加（あるいは変更）したもので，プログラム中に ‘C2024-11-1 CU…’ と書かれている行以降の複数行が追加した部分である．なお，CU のあとの … には 1～9の数字が付けてあって合計9か所あり，それぞれの最初の行の最後尾に ‘…-start’ と示し，また最後の行の最後尾には ‘…^end’ と示してあって，その中間に追加部分が入っている．具体的には，CU1が2行，CU2が8行，CU3が16行，CU4が14行，CU5が4行，CU6が1行，CU7は，573行目～821行目までの249行，CU8は，872行目～983行目までの112行，CU9が15行である．最後のCU9部分は行の先頭にすべて C が付いているので，注釈行となっていて機能しないが，この C を外せば tecplot 用の作図ファイルが作られる (そのままなら，gnuplot 用の作図ファイル)．

CU1の部分は，元のプログラムの配列が，記憶容量節約のために4バイトの単精度実数としてあったものを，8バイトの倍精度実数に変更したもので，U_systemの分子間衝突処理においてエネルギと運動量の保存が正しく行われているかを正確に調べるために変更したものである．

CU2の部分の説明の前に，空間のセルは，二次元平面で整然とした格子状（164×240 の格子であるが，オリフィスより上流の領域を使う場合に備えて，51行目の PARAMETER文では KST9=260, KOT9=240 としている）に配置されており，同じ$x$座標のセルは$y$座標が異なっても同じ横幅を持ち，同じ$y$座標のセルは$x$座標が違っていても同じ縦幅を持っていることをまず覚えておいてもらいたい．そのうえで，UV(i, j, k) は，各セルの左下端 ( j=1~ は，セルの横方向の並びの番号，k=1~ は，セルの縦方向の並びの番号) での流速 $U$ (i=1) と $V$ (i=2) である．ただし，j が最大値になったらセル右端，また，k が最大値になったらセル上端の流速 $U$と$V$になる．同様に，TXY(i, j, k) はセル端での温度 $T_x$ (i=1) と $T_{yz}$ (i=2) である．AUV(i, j) はセルの $x$方向並び ( j=1~ ) の左端座標 (i=1) と 横幅 (i=2)，BUV(i, j) はセルの $y$方向並び ( j=1~ ) の下端座標 (i=1) と縦幅 (i=2) である．以上のものは，式(6)の双線形補間法を使う際に必要である．AV2(3) は衝突前のセル内の運動量の総和 (三成分)，ALAM(3) は$\lambda_X$と$\lambda_Y$と$\lambda_Z$，BV2(3) は衝突後の厳密保存前の運動量の総和 (三成分)，UB1 と UB2 は衝突前後の温度の比が 1/3～3 の間に収まるように温度変化に制限を設けるための値，IUSYS は，U_systemを使う場合であっても最初の１回は通常の計算法（Bird法）で計算するので 58行目でゼロとおいて，１回目の計算が済めば 918行目で１に変更する．

CU3の部分は，計算にU_system を使う(IUB=1) か 使わない(IUB=0) かの指定，各種エラーカウンタ IERR3～IERR8 の初期化（ゼロ化），そして，温度と流速の最高値と最低値を調べるための初期設定であるが，最高・最低値の調査結果は今回の計算には具体的に使用していない．

CU4の部分は，AUV が セルの $x$方向並び (1～KS) の左端座標と横幅の計算，BUV が セルの $y$方向並び (1～KO-2) の下端座標と縦幅の計算である．先に示したように，これらは式(6)の双線形補間法の計算に用いる．

CU5の部分は，計算途中のディスプレイ出力で，何回目の計算 (J1) か，その時点の総分子数 (NM)，それまでの総分子数の最大値 (NMM)，各種エラーの回数を出力する．なお，OV は，衝突計算時の相対速度が，あらかじめ設定した最大相対速度より大きくなった回数について，全衝突計算回数で割算したもので，十分小さい確率が保たれていることをチェックするものである．

CU6の部分では，U_systemの1回目あるいはBird法のときは，493行目からの計算となるが，U_systemの2回目以降は，575行目からの計算に移る．

CU7の部分が，U_system計算の本体部分で，全セル数 NC=KS×(KO-2) についてDO_13241のループが繰り返される．579行目の I7 は，セルの$y$方向並びの番号で 1～KO-2 まで変化し，582行目で I7P=I7+1 として，I7 と I7P が各セルの下と上の辺を指し示す．同様に，580行目の J は，セルの$x$方向並びの番号で 1～KS まで変化し，583行目で JP=J+1 として，J と JP が各セルの左と右の辺を指し示す．588行目以降に現れる変数において，AV1 はセル内分子数，AV3 はセル内分子の速度成分の２乗和の総計（セル内分子の運動エネルギの和を意味するが，エネルギにおける 1/2 や分子質量$m$は共通なので省略されている），配列変数 AV2 と BV2 は衝突前と衝突後の各速度成分の総計，AV22 はセル内の流れ速度による運動エネルギを表す．AV1は DO_13241のループ内で一定で，AV3とAV22 は，各セルにおける衝突前の値であるが，同様の衝突後の値は，768～775行目において BV3とBV22 として計算される．606～617行目，また少し後に現れる 642～647行目は，通常の衝突計算（Bird法）と同じものである．
614～641行目は，1個目の分子（Ｐ分子）に関し，式(6)を用いてその場所の温度$T_x$, $T_{yz}$ と速度$U$, $V$ を求めたもの（ここで使われるセル4隅の流速と温度については，ずっと先の 872～982行目で計算される）．643～668行目は，2個目の分子（Q分子）の場所で同様に求めたものである．671～692行目において，上記で求めた２つの場所の温度の比を計算するが，その値が1/3～３の範囲に収まるように制限をかけ（範囲を超えたらエラーカウントも進める），その後に平方根を求める．このように求めたデータを式(4) に代入して，Ｐ分子をＱ分子の場所に移したときに得られる分子速度成分を求める（694～696行目）．
699～748行目は，修正されたＰ分子の速度を用いて，従来の衝突計算と同じ方法で衝突後の分子速度を求めたもので，その後，750～763行目において，式(5)を使ってＰ分子を元の位置に戻すのに伴う速度変更を行い，最後は配列変数にそれを記憶して終わる．

768～817行目が，Pareschiらの提案した運動量とエネルギの厳密保存の計算で，これにより，衝突後の分子速度が最終的に決定まる．768～775行目に現れる BV3 はセル内分子の速度成分の２乗和の総計（セル内分子の運動エネルギの和を意味するが，エネルギにおける 1/2 や分子質量$m$は共通なので省略），BV2 は衝突後の各速度成分の総計，BV22 はセル内の流れ速度による運動エネルギを表し，いずれも衝突後の値である．なお，同様の衝突前の値は，596～604行目において AV3, AV2 およびAV22 としてすでに計算されている．777～787行目において，これらの値を 式(12)～(17) に代入すれば，速度修正に用いる 4つのパラメータ $\tau$, $\lambda_X$, $\lambda_Y$, $\lambda_Z$ が得られ，式(7) を使って分子間衝突後の最終的な分子速度が決定される．
790～817行目は，運動量とエネルギが確かに保存されているかどうかをチェックしている箇所で，私が適当に定めた許容範囲に入っていない場合にはエラーカウンタが進められ，計算途中でその数が表示される．

CU8 の 872～982行目で，セルの4隅の流速と温度を求めているが，これは，101行目の K100 で指定した回数ごとに更新が行われる．まず，872～916行目において，セル中心の流速と温度が計算されるが，その中で求められている温度と流速の最高・最低値については今回は利用していない．923～947行目は，各セルの下端と上端のデータを求めたもの，949～968行目は，各セルの左端と右端のデータを求めたものである．少し分かりづらい箇所もあるが，読者自身で判読してほしい．970～975行目は，オリフィスの壁面に沿ったセル左端のデータで，流速はゼロ，温度は 288K としている．977～982行目は，オリフィスの孔に沿ったセル左端のデータで，オリフィスから流入する流れの条件（流速と温度）を与えている．

Fortranのソースプログラムに関連して，DSMC法の並列計算コードを公開してほしいとの要望があるが，今のところ公開についての明確な予定はない．なお，並列計算の方法については，参考文献10 において，十分にヒントになることが記載されているので，これを参照してほしい．ただし，参考文献10 での説明がプログラム並列化の最終形ではなく，その後も改良は行われている．例えば，当初「分子並べ替え処理」に必要だった「セル数×スレッド数」の配列要素は，もうそれを使わなくてもよいものができているし，今後，現在の私の並列化プログラムよりも優れたものが現れる可能性は十分ある．このHP（ブログ）に掲載されている３つの実行用プログラムは，全て並列計算ができるようになっているので，その計算速度と比較することにより，読者各自の作成したDSMC法の並列化プログラムのレベルがどの程度であるか，おおよそ判断することはできるであろう．

最後に，U_systemという名称であるが，その U が，先に述べたような Uターンという意味ではなく，私の名前 Usami の U から取ったのではないかと勘繰りを入れる人がいるかも知れない．下賤な私をよく知る人からすればもっともな話である．しかし，これに関しては下記と同様のことを言っておきたいと思う．日本の文豪「森鴎外」の小説「雁」に登場する絶世の美女「お玉」のその後について，僕（鴎外）の情人になったのではないかと訝しがる人に対して，小説の最後で鴎外は次のように述べている．「読者は無用の憶測をせぬが好い．」