(Click here for explanation in English.)
本5.1節のDSMC法の解説は,私の在職中に,大学での教育資料,学会の分科会資料等としてまとめたもので,日本機械学会編の計算力学ハンドブックⅢ(参考文献3)にも同様の内容が掲載されている.最初の資料配布から20年以上経過していて最新情報には乏しいが,このHP(ブログ)に登場してくる内容を理解するために必要な事項が数多く含まれている.元の記述から部分的には修正しているが,主として,DSMC法の創始者であるBirdの著書(参考文献1, 2)やBirdの論文(参考文献12, 13, 14)に基づいて書かれているので,本節では U_systemやプログラムの並列化については触れていない.
DSMC法の基礎
1.はじめに
直接シミュレーションモンテカルロ法(DSMC法)は,1963年 Bird により,希薄気体流の数値計算法として開発された.計算機内に多数の分子の位置座標と速度成分を記憶し,それら分子の「空間移動」と「分子間衝突」を微小時間ステップで分離して,交互に計算を繰り返すことにより流れ場を解析するものである.この手法は,1976年に出版された Bird のDSMC法に関する著書(参考文献1)によって世界中に広く知られるものとなり,1994年には大幅に書き改められた改訂版(参考文献2)が出て今日に至っている.その間,分子モデルおよび衝突モデルには大きな進展があり,また,計算機技術の進歩と相まって,三次元解析はもとより,分子流から連続流にわたる広い領域での利用が可能になった.さらにこの手法の微視的解析という特徴を生かして,流体不安定現象の解析に適用する試みもある(本HPの第3章,第4章を参照).ここでは,DSMC法の基礎を解説するにあたり,例題として「軸対称場における超音速希薄自由噴流」を取り上げ,その Fortranプログラム(簡易版)を参照しながらDSMC法の詳細を眺めていく.Fortran言語は命令数が非常に少なく(変数の型,入出力文,代入文,ブロックIF文,DOループ,GOTO文,副プログラムの7つを理解すればよく,VBA言語に近いものであるが,基本的にコンパイラ方式なので計算は速い),初心者でも比較的短時間に習得できるので,DSMC法を理解するのに有効である.
<宇佐美の教育資料>Fortran77固定形式3時間マスターは,ここをクリック.
DSMC法では,プログラムの多くの部分が,対象とする問題に依存せず共通に使えるので,本節における例題を核として,様々な流れ場へ適用してもらえるものと考える.また,単原子気体から多原子気体へ,単一気体から混合気体へ,さらには化学反応を含む流れまで,この例題を発展させることも可能であろう.詳細は,追って順に眺めていくことにして,まずは,DSMC法の計算手順の概要とその特徴から列記してみる.
2.DSMC法の計算手順の概要
[1]分子は,まず,乱数により初期座標と初期速度成分を与えられて,対象となる物理空間に配置される.その物理空間は,セルと呼ばれる微小空間に分割されている.セル一辺の大きさは,理想的には,局所的な平均自由行程よりも小さくとるのがよい.
[2]「分子の物理空間内での移動(固体壁との衝突および流入流出境界での出入りを含む)の計算」と「分子間衝突の計算」は,微小時間ステップ$\Delta t$(これは局所的な平均衝突時間よりも小さくとることが理想的)で分離され,独立に計算が行われる.すなわち,以下の3段階の過程が繰り返される.
a.各々の分子は,その速度に応じて$\Delta t$時間だけ,他の分子とは独立に空間を移動する.その際,壁表面での反射あるいは境界からの流出が生ずれば,運動量とエネルギーの収支が計算される.また,境界から新しく分子が流入する.
b.分子移動によって各々の分子の位置座標が変化するので,分子の所属するセルが調査され,分子間衝突の準備として,「参照用配列」上で全分子の並べ替えが行われる.すなわち,各セルには,その中に存在する分子数だけの連続した番号(座席番号)が,配列の添字として与えられ,その配列要素に分子番号が記憶される.衝突計算において,あるセルに属する座席番号が一つ決まると,その番号から,この配列を用いて分子番号が参照され,分子の速度成分等の情報を引き出すことができる.
c.分子間衝突は,衝突の法則に基づき,セルごとに計算が行われる.$\Delta t$時間内に生じる衝突数の算定,衝突ペアの選択および衝突後の速度成分の決定が主な内容である.なお,衝突計算において,セル内での分子位置に関する考慮は行われない.一方,5.2節で解説されるU_systemでは,分子のセル内位置に応じて衝突前後の分子速度に補正が加えられるので,セルを大きくとることができる.
[3]上記の a~c の過程が繰り返され,流れ場の諸量について,非定常問題にあってはアンサンブル平均が,定常問題にあっては定常状態達成後の時間平均が計算される.なお,アンサンブル平均は,セルあたりの分子数が少ないのを補うために行われるが,空間的に変化が少ない範囲のセルを平均したり,時間的に変化の少ない範囲の時間平均をとる等をすれば,アンサンブル平均を行うことなしに非定常解析を行える.3.1節や4.2節に示したアニメーションは,このようにして求めたものである.
3.DSMC法の特徴(長所と短所)
[1]個々の分子の運動に基づいて計算するので膨大な時間がかかる欠点がある.DSMC法の得意分野は,希薄気体,高速気体であるが,密度が高い場合(と言っても1気圧以下ではあるが),またそれが低速の場合には,定常状態達成までに長時間かかり,解析はより困難になる.分子の最大確率速度が350 m/sであるとした場合,その分子運動を基に流れの解析が行われるので,結果の統計的変動を低く抑えるために,例えば1 m/sといったような低速の現象の解明にはサンプル分子数(あるいは計算の繰返し回数)を相当量多く必要とする.ただし,解析対象が流速でなければ,静止した気体であっても解析はできる.
[2]境界条件が与え易い.例えば,固体壁面では分子の反射法則を与えるだけでよく,しかも工学計算では,簡単な拡散反射(散乱反射)で十分な場合が多い.流入境界における分子の流入位置と速度成分の算出,あるいは,流入分子数の算定も,巨視的状態量に応じて容易に決めることができる.DSMC法において流入流出境界に与えられる条件は,境界から流入する分子のみに適用されるものであって,計算領域から流出する分子に対しては直接適用されない(もちろん,境界から流入した分子との衝突により間接的には影響を受ける).したがって,境界条件に無限遠のような極端な状態を与えたとしても,流出分子はそれに厳密に拘束されることはなく,計算が発散するようなことはない.もちろん,流入分子と流出分子の巨視的状態に差のない方が境界条件としては好ましいので,そのための方策は重要である.なお,両者に差異があると境界付近の流れ場に歪みを生じるが,領域全体の結果が全く無意味になるものではない.
[3]DSMC法は時間の経過とともに計算が進行するので,本質的に非定常計算である.よって,定常問題と非定常問題とで計算の難易度に本質的な違いはない.このことは,定常問題の解法であっても,非定常状態を経過した上でないと解が求められないことを意味する.
[4]流れ場のセル分割(格子切り)が容易である.分子の空間移動は,セル構造とは無関係に行われるので,必ずしも境界形状に沿ってセル分割を行う必要がない(詳細後述).
[5]新しくプログラムを作る際の主な部分は,セル分割と分子移動のルーチンである.分子間衝突に関する部分は既存のルーチンがそのまま利用できる.ただし,分子移動のプログラム作成は経験を積まないと困難を極める.
[6]希薄気体流のみならずミクロ流の解析に利用できる.DSMC法は,希薄気体流の数値解析法として開発された.例題で示すように,今日では,分子流から連続流まで大きく状態変化する領域でも用いられるようになっており,今後は大気圧の流れにも適用できる改良がなされるであろう.一方,ミクロ流の世界では,DSMC法は大気圧でもそのまま利用できる.希薄度を表す無次元数はクヌッセン数 \(K_n\) であり,平均自由行程 \(\lambda\) と代表長さ \(L\) を用いて次のように定義される.
\begin{equation}K_n=\lambda /L\end{equation} \(K_n\) が大きいほど希薄度は増し,DSMC法で解析しやすい領域となる.希薄気体というと一般的には,低密度,すなわち \(\lambda\) が大きい状態を指すが,\(\lambda\) が小さくとも \(L\) がそれ以上に小さければ \(K_n\) は増加する.これがミクロ流である.
4.例題の概略
DSMC法の基礎を説明するにあたり,例題として「軸対称場における超音速希薄自由噴流」を取り上げ,Fortranプログラムを参照しながら解説を進める(プログラムリスト参照にはここをクリック:プログラム各行の左側の1桁~3桁の数字とそれに続く空白1つは,行番号(1~677)を示したもので,プログラムには含まれないことに注意).なお,本文中で Fortranプログラムの変数を記述する際には,誤解を避けるために,変数記号にアンダーラインを付けることにする(例えば,TEMP).例題は,700行程度の非常に簡素化されたプログラムであるが,基本的事項はほとんど備えている.図1に示すように,半径EZA(実半径は0.00125 m)の円形オリフィスを持つ厚みゼロの壁と,その右に広がる空間(計算空間)から成る単純な流れ場で,オリフィス(円形孔と壁面)以外は,流入流出境界(下流背圧に相当する密度を持つ境界で,今後これを下流境界と呼ぶ)が流れ場を取り囲んでいる.下流境界は,「中心軸に平行な境界(周囲境界)」と「中心軸に垂直な境界(垂直境界)」に分けることもできるが,単に下流境界と呼んだ場合は両者を指す.

軸対称場なので中心軸(噴流中心軸)より上だけで計算空間を表現する.セル分割は2次元であるが,流れ場は3次元の広がりをもつ.オリフィス孔断面で流速は一様で音速 (\(M=1\)) に等しいと仮定し,上流よどみ点から等エントロピ変化により流れがオリフィス孔に達したものとして,そこでの密度と温度を決定する.下流周囲境界での巨視的流速はゼロと仮定し,下流垂直境界での巨視的流速は,計算進行とともに変化する境界付近の分子の速度を平均して決める.また,オリフィス壁面で分子は拡散反射する.気体は単原子分子のアルゴン単一気体とする.流れ場の初期密度は,下流境界の値に等しくし,時刻ゼロで,オリフィス孔より気体が流入し,超音速噴流が完成するまでをシミュレーションする.このプログラムでは,変数は全てSI単位で数値が与えられている.上流よどみ点の圧力は 6700 Pa(50 Torr),下流背圧はその 1/50(1 Torr)で,温度はともに15℃である.噴流構造を正確に再現するためには,オリフィスより上流側にも計算空間を設ける必要があるが,今回の簡易プログラムでは省略している.
5.特定分布の乱数発生
ここでは,0.0~1.0まで一様に分布する実数乱数(以降,一様乱数 \(R_f\) と記述)を用いて,DSMC法の計算で必要な特定分布の乱数を作成する方法を3種類紹介しておく.
[1]逆変換法(直接法)
特定の分布関数 \(f_0\) を,有効な全領域(全区間 \(a\)~\(b\))で積分したときの値を \(A\) としたとき,分布関数 \(f_0\) を \(A\) で除して得られる分布関数 \(f\) を,正規化された分布関数と呼ぶ(全領域を積分して1となるような分布関数と考えてもよい).
\begin{equation}f=f_{0}/A, A=\int_{a}^{b}f_{0} dx\end{equation}
さらに,\(f\) を \(a\) から任意の値 \(x\) まで積分したものを累積分布関数 \(F_x\) と呼ぶ.
\begin{equation}F_x=\int_{a}^{x}f dx\end{equation}
累積分布関数 \(F_x\) を \(R_f\) と等しいとおいて,これが \(x\) について陽に解けたなら,すなわち,\(x=g(R_f)\) と書けて \(R_f\) から \(x\) が計算できたなら,一様乱数 \(R_f\) から特定の分布 \(f_0\) に従う乱数 \(x\) が得られたことになる.例えば,分子が半径 \(r_0\) の円の中に一様に分布するとして,その中の一つの分子の,円中心からの距離 \(r\) を求めたい場合(これは,本節の例題において,オリフィス孔から流入する分子の位置座標 \(y\) を求める場合,および,中心軸に垂直な下流境界上で分子を発生する場合に相当する),その分子位置の確率は \(r\) に比例するので,累積分布関数を求めると次のようになる.
\begin{equation}F_r=\int_{0}^{r}2r/r_0^2 \ dr=r^2/r_0^2\end{equation} これを一様乱数 \(R_f\) に等しいとおいて解くと次式が得られる.
\begin{equation}r=r_0\sqrt{R_f}\end{equation}
<課題>内球の半径$a$,外球の半径$b$の球殻の中に分子が一様に分布する場合,分子の球中心からの位置を一つ発生せよ.
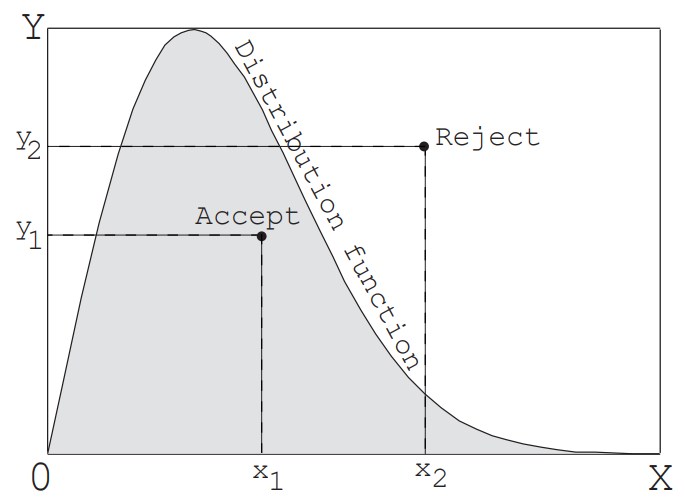
[2]棄却法
前述の逆変換法は,累積分布関数と$R_f$を等号で結んだ式が陽に解けないと使うことができない.これに対し,図2に示すように,任意の分布関数を長方形で囲み,長方形の横幅$X$と縦幅$Y$について乱数を各々1つ求めることにより,その分布関数に従う値を発生することができる.すなわち,2つの乱数により長方形の中に1点$(x,y)$が定まるが,その点が分布関数の下(分布の中)に位置すれば,その点の$x$が求める値となる.もし点が分布の外に落ちたなら,再度,乱数を横と縦に発生して1点を求め,点が分布の中に落ちるまで繰り返す.この方法は,任意の分布について適用できるが,一つの値を求めるのに2個以上の一様乱数$R_f$を使う必要がある.特に,分布関数内側の面積が長方形面積にくらべて小さくなるほど効率は悪くなる.そこで,例えば平衡状態の分子速度分布のように,理論上は無限大の速度まで存在するが,速度が大きくなるほど確率はゼロに近づくといった分布については,打切り値を設けて幅を制限する必要がある.本節の例題では,オリフィス孔から流入する分子の速度成分(孔面に垂直な速度成分)の発生にこの方法を用いる.その詳細は後述する.
[3]正規分布する値を2つ同時に求める方法
平衡状態における分子速度分布関数のように,正規分布する値を2つ同時に求める効率のよい方法がある.いま,平衡状態にある$x$方向の速度成分$u’$(分子の実際の速度から巨視的流速を差し引いた熱運動速度の$x$成分)の分布関数を$f_{u’}$,$y$方向の分布関数を$f_{v’}$とする.
\begin{equation}f_{u’}=\frac{\beta}{\sqrt{\pi}} \exp(-\beta^2 u’^2), f_{v’}=\frac{\beta}{\sqrt{\pi}} \exp(-\beta^2 v’^2)\end{equation}
ここで,$\beta$は,分子の最大確率速度$c_{max}'(=\sqrt{2RT})$の逆数,$R$は気体定数,$T$は絶対温度である.なお,これら速度分布関数は正規化されている.二つの分布関数を掛け合わせると,
\begin{equation}f_{u’} du’ \times f_{v’} dv’ =\frac{\beta^2}{\pi} \exp\{-\beta^2 (u’^2+v’^2)\} du’ dv’\end{equation}
ここで,次のように変数$u’, \ v’$を$r, \ \theta$に置き換えると
\begin{equation}u’=r \cos \theta, \ v’=r \sin \theta\end{equation}
\begin{equation}f_r dr f_{\theta} d\theta =\frac{\beta^2}{\pi} \exp(-\beta^2 r^2)r dr d\theta = \frac{1}{2\pi} \exp(-\beta^2 r^2) d(\beta^2 r^2) d\theta \end{equation}
したがって,$f_{\theta}=$Const., $f_{\beta^2 r^2}=$Const.$\times \exp(-\beta^2 r^2)$ となり,積分範囲は,$\theta=0\sim 2\pi$,$\beta^2 r^2=0\sim \infty$ である.ここで前述の逆変換法を二者に適用すると,
\begin{equation}\theta=2\pi R_{f1}\end{equation}
\begin{equation}r=\sqrt{-\log_e (1-R_{f2})}/\beta\end{equation}
となるが,一様乱数の性質から $R_{f2}$と$1-R_{f2}$ は同じなので,
\begin{equation}r=\sqrt{-\log_e R_{f2}}/\beta=\sqrt{-2RT\log_e R_{f2}}\end{equation}
すなわち,異なる二つの一様乱数$R_{f1}$と$R_{f2}$から,式(8)(10)(12)を用いて,速度成分$u’, v’$を同時に求めることができる.なお,この平衡状態の分子速度発生式は,分子が壁面で拡散反射するときの,壁面に平行な速度成分の計算にも適用することができる.もちろんその場合の$\beta=1/\sqrt{2RT}$には,壁面温度に相当する値を用いる.
6.関数副プログラム
例題のプログラムでは,主プログラム以外に,先頭に3つの副プログラムが付属している.最初の RANF0() は,合同法による一様乱数生成の関数で,周期は$2^{29}$である.この乱数の元となる整数乱数の初期値は,例題プログラム52行目(以降の記述で○行(目)とあるのは全て例題プログラムを指す)にある IRAN の値で,この値は,奇数であれば何でもかまわない.乱数初期値を変更したい場合は,ここを任意の奇数値に置き換えればよい.他に信頼できる一様乱数ルーチンがあればそれを用いるのもよいし,可能なら64ビット整数による周期の長い乱数を使うのが望ましい.
二つ目の副プログラム GAM(X) は,ガンマ関数を求めるもので,チェビシェフの級数を用いて近似計算する.これはVHSおよびVSS分子モデルの計算に使用する.三番目の ERF(X) は誤差関数を求めるもので,分子の流入部に巨視的流速が存在する場合,流入分子数を算定するために使用する.例題では,オリフィス孔からの流入分子数を算出するのに用いている.この誤差関数の計算式は,Abramowitzらの式を用いる.
7.DSMC計算で使用する配列変数
DSMC法で用いる実数変数には,基本的に倍精度実数(IMPLICIT文参照)を用いる.分子の空間移動における誤差を最小限に抑えるためである.ただし,分子あるいはセルの情報を記憶するための配列は大量となるため,例題では,これら大型配列には単精度実数を用いている(PCにメモリが十分搭載されていれば,そのまま倍精度配列を用いるに越したことはない).すなわち,分子速度成分 P(3,MOL),位置座標 PZ1(MOL),PZ2(MOL) とセル体積 CTA(NCELL)である.なお,MOL は最大分子数,NCELL は最大セル数であり,計算機容量に応じてPARAMETER文の数値を変更すれば,さらに多くの分子数,セル数を扱うことができる.LCR は,分子間衝突計算で使用する参照用配列,IP は,分子の所属するセル番号を記憶する.なお,例題は軸対称計算であるため$z$座標 PZ3 は必要ないが,三次元計算の場合は必要になる.IC1 にはセル内分子数を記憶,IC2 には,参照用配列における各セルの先頭番地から1を引いたもの(先頭番地$-1$)が記憶される(詳細は後述).本プログラムではセル中心の座標を配列変数として記憶することはせず,必要なときにその場で算出する方法をとる.なお,三次元問題になるとセル数が極端に増加するので,セル内分子数を小さくせざるを得ないが,もしその個数が 127以内に収まるなら,IC1 を1バイト整数にしてメモリを節約する工夫もできる.SC(8,NCELL) は,各セル(サンプルセル)の巨視的物理量を算出するための原情報を記憶する配列である.本例題では,分子間衝突のためのセル(衝突セル)とサンプルセルは同じものを用いているが,もし衝突セルの数が大きくなった場合には,衝突セルを幾つかまとめてサンプルセルとし,この配列を節約することもできる.SS は,境界から流入流出する分子数を記憶する.この他,一般的には,壁面反射時に運動量およびエネルギの収支を記憶する変数が用いられるが本例題では使用しない.
OP および ASC は作業用の配列,一連の文字型変数は,結果を出力するためのファイル名を記憶するためのもの,PRI は境界での流量(無次元コンダクタンス)を記憶する配列で,U0 は下流垂直境界における流速の推定値である.
8.例題(超音速自由噴流)プログラムの開始
IERRx は,計算途中でのエラーの数を調べるカウンター,RVRALL と RVRGT は,分子間衝突における最大衝突数の良否を検査する変数,IRAN は整数乱数(奇数),PI は円周率である.
上流よどみ点の温度 TEMP およびオリフィス壁温度 TEMPW は15℃,圧力 PTOR は50Torr,PPAS は[Pa]単位で表示した圧力,ANUM は数密度$n$ [1/m$^3$],PRAT は上流よどみ点圧力と下流背圧との比(圧力比)で50である.オリフィス直径 ORID は0.0025mである.
DSMC法では,分子移動と分子間衝突を時間ステップ$\Delta t$で分離して計算を繰り返すが,これを NIS 回繰り返したところで,セルの原情報のサンプリングを行う.これが一回のRUNとなる.ただし今回の NIS は1である.一回のRUNを K100 (=5000) 回繰り返したところで,セル内の原情報を平均してファイルに出力する.出力ファイル名の先頭4文字は’sjet’である.I9 は計算打切りのためのRUN数で,今回は100000回で計算を終了する.すなわち,出力ファイルは20個作られる.
9.流れ場のセル分割
流れ場を分割するセルには二つの役目がある.一つは,分子間衝突が同一セルに存在する分子間で行われることで,他の一つは,密度,速度,温度といった流れ場情報をサンプルするための微小要素としてセルが使われることである.同一セル内の分子は,その相対位置に関係なく衝突計算にかけられるので,理想的には,セル一辺の長さは局所平均自由行程よりも小さくとるべきである.しかし,軸対称あるいは三次元問題においては,流れ場の広さとその密度が大きくなるとセル長を平均自由行程以下にすることは難しく,計算機容量の制限で,やむを得ずセルを大きくとることがある.しかし,セルを大きくした場合でも,得られる結果が全く信頼できないものになるわけではなく,密度,温度等,物理量の変化割合が本来あるべきものよりも幾分緩和された形となって現れるに過ぎない.したがって,状態変化が緩やかな場所ではセルは大きくできるし,一方,変化が急峻な場所でセルを大きくした場合には,本来の変化よりも多少緩和された結果が得られるということを銘記してDSMC法を用いればよい.セル分割の方法で最も単純なのは,空間を矩形のセルで分割することである.たとえ境界が任意の曲面であってもセル分割は矩形で行える.何故なら,セルは分子の空間移動に全く関与しないからで,矩形のセル構造であっても,分子の運動は境界形状に矛盾せず行われる(セル体積については,実際に気体が存在する空間の体積を求めておく).複雑な境界形状の場合,幾つかのセルの体積が極端に小さくなり,そのセル内に分子が殆どなくなって衝突計算に支障をきたすのでは,と危惧することがあるかも知れない.しかし,近傍に存在するセルが相当数まとまって小さくならない限りその影響は現れない.
Bird(参考文献12)は,1987年,渦生成に関する分子動力学法(MD法)との算法の比較において,サブセル分割法を考案した.当時分子間衝突法で主流を占めていたタイムカウンタ法(TC法)においてはセル内に20個以上の分子を含む必要があったため,その数を確保し,かつ衝突分子間距離を平均自由行程以下に保つため,通常のセル格子の中をさらに細かなセルで分割したものである.しかし,現在一般的に用いられている最大衝突数法(Null-collision法,No-time-counter法)では,セル内分子数が1程度でも理論衝突数を満たすので(参考文献15),サブセル法の果たす役割は当初ほど重要ではない.なお,Birdの著書(参考文献2)に示されたサブセル法のプログラムコードは1次元計算用に作成されているので,2次元あるいは3次元問題に適用した場合には必ずしも正確な計算とはならない.最近,宇佐美ら(参考文献3, 4, 5)は,セル内の分子位置を考慮して衝突計算を行なう手法 U-system を開発した.セルを平均自由行程よりかなり大きくしても非常に良い結果が得られるこの手法の詳細については 5.2節で解説する.
例題の自由噴流は下流に進むにつれて急速にその密度を低下させるので,流れ場を細分するセル構造(軸方向のセル分割)としては,下流にいくほどセル長を等比級数的に増加させる方式をとり,各セルの分子数に大きな差異を生じないようにする.すなわち,中心軸上において,オリフィス直後のセル一辺の長さを $a$(Fortran変数は TKN),公比を $b$(ES0)として,$i$ 番目のセルの長さを$ab^{i-1}$とする.この場合,もし分子の座標が $x$であるならば,その分子の所属するセルの軸方向番号$j$は,
\begin{equation}j=\frac{\log \{x(b-1)/a+1 \}}{\log b}+1 (小数点以下切捨) \end{equation} と簡単に計算できる(参考文献16).今回,軸方向のセル数 KS は164,公比 ES0 は1.02とした.一方,半径方向のセル分割は,基本的には,まずオリフィス半径 EZA が,長さ TKN のセル40個(I2)で等分割されており,流れ場の半径方向全体のセル構造についても等分割で,分割数 KO は240となっている.
82~83行の AL1 と AL2 は,式(13)の中の $(b-1)/a$ と $1/\log b$ である.
なお,軸対称場において半径方向を等分割にすると,中心軸上のセル体積は極端に小さくなり十分な分子数を確保できない.そこで例題では,中心軸上のセルのみ,径方向に隣接する三つのセルを結合して一つのセルとする操作を行っている.
セルの体積 CTA は87~104行の二重のDOループで計算している.軸対称流れ場なので,中心軸上以外のセルは環状構造になる.中心軸に最も近い三つのセルは結合されて一つになるので,若干複雑なルーチンになっている.また,全セル数 NC は,KS$*$(KO$-$2) となる. なお,中心軸上のセルは三つ結合しているが,「基準セル」としては,結合する前のオリフィス直後の中心軸上セルを用いる.シミュレーション分子の重み係数(後述)等は,この基準セルを使って説明される.基準セルの体積は特に CH として記憶し,TKN$*$TKN$*$TKN$*$PI である(109行).
<課題>矩形セルで格子状に分割されている流れ場の中に,厚みゼロの板が斜めに置いてあり,いくつかのセルが,板の表と裏に分断されている.このような場合,板に分断されたセルをどのように扱ったらよいか考察せよ.
10.セル内分子数とシミュレーション分子の重み係数
気体の分子数は,1モル$6\times 10^{23}$個であり,たとえかなりの希薄状態であっても計算機内で実気体と同じ個数の分子を運動させることは難しい.一方,DSMC法は統計計算である.全ての分子の運動を解析せずとも,その一部分を抜き取って(サンプルあるいはサンプリングして)分子全体の動きを予測する.例えば,流れ場のある場所(セル)を100万個のサンプル分子の平均値で解析したとすれば,約$\pm 0.1$%の誤差で信頼できる結果が得られる.さて,この100万個のサンプル分子であるが,ゼロ次元問題の場合にはセル1個でよいから問題なく計算できるが,このセル自体が例えば100万個あるような3次元問題では総計$10^{12}$個となるので,筆者が使える計算機システムではとうてい困難である.そこで,例えば,一回の計算としてはセルに10個の分子を入れて解析し,それと同じ計算を10万回繰り返すことにより,結果として100万個のサンプル分子を確保するという手段が用いられる.それでは一回の計算におけるセル内分子数はいくつまで減ずることができるであろうか.これについては,問題に依るので必ずしも一概には言えないが,例題で示す超音速自由噴流の場合には,時間平均で,セル内に分子が1個以上あれば一応の結果が得られるという報告がなされている(参考文献15).なお,セルあたり1個というのは極端な場合で,個人的には,4個以上あるのが望ましいと考える.
このように実気体の分子数がいくらであっても,DSMC法における分子数をかなり自由に決めることができるが,シミュレーション分子1個がいったい実分子何個を代表しているかは記憶しておく必要がある.これを重み係数 WEI と呼ぶ.すなわち,時間ステップ$\Delta t$あたりの分子間衝突数の算定において,見かけ上,衝突断面積$\sigma_T$は,分子数の減少に反比例して大きくなる必要があり,この重み係数を用いて修正する.なお,「シミュレーション分子そのものが大きくなり,重み係数に相当する個数をひとまとめにした巨大分子が計算空間を運動する」と考えるのは正しくない.あくまで,シミュレーション分子は,多数ある実分子からサンプリング(抜取検査)されたもので,実分子と同じ大きさ同じ質量を持つと考えられるべきである.
例題で,上流よどみ点の実分子数密度は ANUM[1/m$^3$]である.それゆえ,基準セル体積 CH 中の分子数は,密度がよどみ点における値であるとしたとき BNUM となる(110行).シミュレーションではこのセルの中に AMC(=0.5)個の分子を入れるので(75行),重み係数 WEI は111行目で求められる.なお,オリフィス直後はよどみ点より密度が低いけれども,中心軸上のセルは3つ結合するので分子数は1を超える.
<課題>セル内分子数が時間平均で1個の場合,衝突相手が見つからないのではという疑問が生ずる.しかし,シミュレーションは成立する.このことについて考察せよ.
11.分子モデル(VHS分子とVSS分子) – 衝突計算その1
DSMC法で著しく改良されたものの一つが分子モデルである.初期のころ(参考文献1)は,計算速度を優先するなら剛体球分子を,実分子への忠実度を優先するなら逆べき乗分子(Inverse power law molecule)を使用していた.その後 Birdは,数多くの計算結果の分析から,「逆べき乗分子が良好な結果をもたらすのは,衝突計算において偏向角を忠実に再現しているからではなく,衝突断面積が相対並進エネルギの関数になっていることによる」との結論を得るに至った.そして1981年の論文(参考文献13)において,衝突力学は剛体球散乱法則(剛体球分子の衝突において,衝突後の相対速度は確率的に優位な方向がない)を維持しながら,衝突断面積を相対速度の関数にするというVHS分子モデルを発表した(すなわち分子直径が相対速度の関数となる分子モデル).剛体球とほぼ同様な衝突力学であるため計算速度に優れ,かつ,逆べき乗分子に近い計算効果を上げる分子モデルである.
いま,温度$T_{ref}$,粘性係数$\mu_{ref}$を基準状態における値とすると,VHS分子の基準直径は次式で計算できる.
\begin{equation}d_{ref}=
\sqrt{ \frac{5(\alpha +1)(\alpha +2)(mkT_{ref}/\pi)^{1/2}}{4\alpha(5-2\omega)(7-2\omega)\mu_{ref}} }
\end{equation}
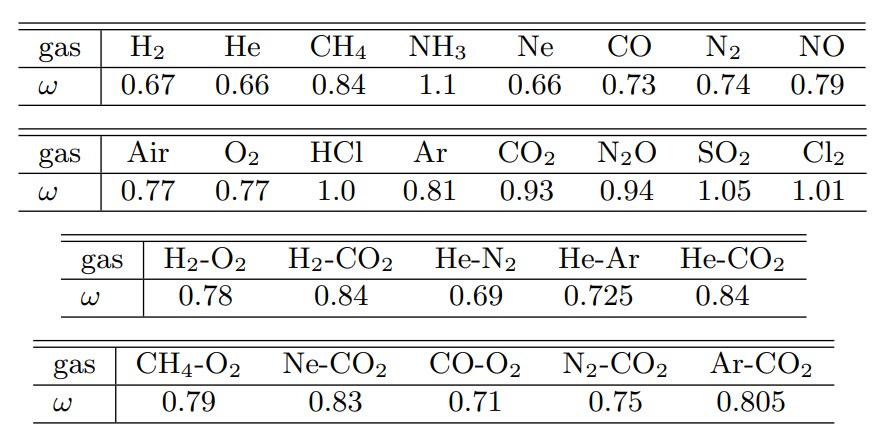
ここで,$m$は分子質量,$k$はボルツマン定数,$\omega$は粘性係数の温度指数で,$\alpha$は 1 とする.なお$\omega$は,粘性係数の温度依存性を実験により求めて決定される.表1にいくつかの気体の$\omega$の値を示す(参考文献2).
Table 1 粘性係数の温度指数 ω
さて,基準衝突断面積$\sigma_{Tref}$は次式となる.
\begin{equation}\sigma_{Tref}=\pi d_{ref}^2\end{equation}
さらに,分子間衝突における相対速度を$c_r$,換算質量を$m_r(=m_1 m_2/(m_1+m_2))$とすると,その場合の衝突断面積$\sigma_{T}$は,次式で求められる.
\begin{equation}\sigma_{T}=\sigma_{Tref}\{2kT_{ref}/(m_rc_r^2)\}^{\omega-0.5}/\Gamma(5/2-\omega)\end{equation}
ここで,$\Gamma$はガンマ関数である.
衝突確率は,衝突断面積と相対速度の積に比例するのでその積を求めると次式となる
\begin{equation}\sigma_{T}c_r=\sigma_{Tref}\frac{(2kT_{ref}/m_r)^{\omega-0.5}}{\Gamma(5/2-\omega)}\ c_r^{2(1-\omega)}\end{equation}
なお,VHS分子の直径$d_{ref}$を用いると平均自由行程$\lambda$は次のように計算できる.
\begin{equation}\lambda=\frac{1}{\sqrt{2} \pi d_{ref}^2n(T_{ref}/T)^{\omega-0.5}}\end{equation}
クヌッセン数$K_n$はこの$\lambda$の値から求める.VHS分子の衝突力学は剛体球のそれと全く同じである.すなわち,衝突の前後で相対速度の絶対値 $c_r$ は変化せず,また,衝突後の相対速度の方向に指向性(確率的に優位な方向)はない.したがって,その方向は立体角に比例するように選べばよい.いま速度空間を極座標で考え,速度ベクトルの極角を$\theta$,方位角を$\phi$とすると,この極座標の立体角の要素は $\sin\theta d\theta d\phi$ となる.したがって方位角$\phi$は $0\sim 2\pi$ の範囲に一様分布し,極角$\theta$は $0\sim \pi$ の範囲を分布関数 $f_\theta=\sin\theta$ で分布することになる.これを変形すると次の式を得る.
\begin{equation}f_\theta d\theta=\sin\theta d\theta=-d(\cos\theta)=f_{\cos\theta}d(\cos\theta)\end{equation}
すなわち,$\cos\theta$は $-1\sim 1$ の範囲で一様に分布する.求めるべき衝突後の相対速度の三方向成分は,相対速度の絶対値 $c_r$ に $\cos\theta, \ \sin\theta \cos\phi, \ \sin\theta \sin\phi$ を乗じたものであるから,まず $-1\sim 1$ の一様乱数により $\cos\theta, \ \sin\theta$ を計算し,次に $0\sim 2\pi$ の範囲の一様乱数により $\phi$ を求めて $\cos\phi, \ \sin\phi$ を計算すればよい.以上をまとめると,衝突後の相対速度成分 $u_{r}^*, v_{r}^*, w_{r}^*$ は以下のように求められる.
\begin{equation}\cos\theta=2R_{f1}-1\end{equation}
\begin{equation}\sin\theta=\sqrt{1-\cos^2 \theta}\end{equation}
\begin{equation}\phi=2\pi R_{f2}\end{equation}
\begin{equation}u_{r}^*=c_r\cos\theta\end{equation}
\begin{equation}v_{r}^*=c_r\sin\theta \cos\phi, \ \ w_{r}^*=c_r\sin\theta \sin\phi\end{equation}
VHS分子は,その後,古浦と松本(参考文献17)によって,拡散係数も考慮したVSS分子モデルへと改良された.
VSS分子では,衝突断面積はVHS分子と同様に考えるが,衝突による偏向角$\chi$を次式のようにする.
\begin{equation}\chi=2\cos^{-1}\{(b/d)^{1/\alpha}\}\end{equation}
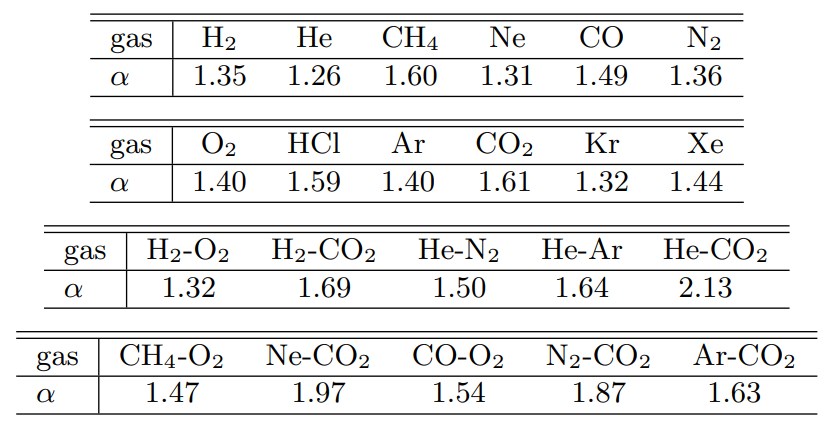
ここで$d$は分子直径(衝突時の実効直径),$b$は衝突パラメータ(質量中心座標系において二つの分子の接近軌跡が衝突によって曲げられないと仮定したときの最接近距離)である.また,VHS分子では$\alpha=1$としたが,VSS分子では$\alpha$を拡散係数の測定値から決定する.表2に代表的な気体の$\alpha$を示す(参考文献2).
Table 2 各種気体の α
VSS分子の基準直径$d_{ref}$は,この$\alpha$を式(14)に代入して求められる.さて,式(25)を次のように書き直す.
\begin{equation}\cos\chi=2\{(b/d)^2\}^{1/\alpha}-1\end{equation}
いま,逆変換法の説明で得られた式(5)と同じように,$b/d$は$\sqrt{R_f}$に等しいとおくことができるので,偏向角$\chi$の余弦は$R_f$から簡単に求められる.
\begin{equation}\cos\chi=2R_{f1}^{1/\alpha}-1\end{equation}
もちろん$\alpha=1$の場合は,VHS分子の式(20)の$\theta$を$\chi$に置き換えたものと一致する.VSS分子の衝突後の相対速度成分は,衝突前の成分を $u_{r}, v_{r}, w_{r}$ として,以下のように計算できる.
\begin{equation}\epsilon=2\pi R_{f2}\end{equation}
\begin{equation}c_{r,yz}=\sqrt{v_{r}^2+w_{r}^2}\end{equation}
\begin{equation}u_{r}^*=\cos\chi \ u_{r}+\sin\chi \sin\epsilon \ c_{r,yz}\end{equation}
\begin{equation}v_{r}^*=\cos\chi \ v_{r}+\sin\chi \ (c_rw_{r}\cos\epsilon-u_{r}v_{r}\sin\epsilon)/c_{r,yz}\end{equation}
\begin{equation}w_{r}^*=\cos\chi \ w_{r}-\sin\chi \ (c_rv_{r}\cos\epsilon+u_{r}w_{r}\sin\epsilon)/c_{r,yz}\end{equation}
単一気体の場合は,VHS分子とVSS分子で結果にほとんど差異は出ないが,混合気体の計算ではVSS分子に効果が現れると報告されている.ただし計算時間ではVHS分子が有利である.
例題では,アルゴン単一気体を扱うが,VHS分子にするかVSS分子にするかは,IVSS に0か1を代入して決める(113〜123行).AMOL は分子量,RGAS は気体定数,AMAS は分子一個の質量,BOL はボルツマン定数,AMR は換算質量,HNH は比熱比,VISC は粘性係数,DIRM は基準分子直径,ACXS は基準衝突断面積,VM は最大確率分子速度(最確速度),BETA は$\beta$,AVA は平均分子速度,VRM は平均相対速度,AMFP は平均自由行程,DEN0 は上流よどみ点密度,TAU は平均自由時間(平均衝突時間),RRKN は $1/K_n$ で,VMW は壁温における最確速度,BETAW はそれの逆数である.
12.分子間衝突の計算 – 衝突計算その2
DSMC法の発展において最も議論されたのが分子間衝突のモデルである.$\Delta t$あたりの衝突数を算定するには,セル内に存在する全ての分子について相対速度の平均$\overline{c_r}$を求める必要があるが,分子数が多くなるとそれに費やす時間が極端に長くなる.これを避けるために最初Birdはタイムカウンタ法(TC法)(参考文献1)を考案した.TC法は計算スピードが速かったため約20年にわたり使われ続けてきたが,その間たえず,この方法に付随する問題点が,ボルツマン方程式との関連付けも含めて議論されていた.その議論に一応の終止符を打ったのが最大衝突数法(No-time-counter法,Null-collision法)の登場である.筆者の知る限りでは,これをDSMC法に最初に適用したのはHermina(参考文献18)である.その後,ほぼ時を同じくして,Bird(参考文献14)がNo-time-conuter法として,古浦(参考文献19)がNull-collision法の改良版として発表した.これらの手法を考案するに至る経緯と衝突数算定時のセル内分子数の扱いに若干の違いはあるが,結果として同じ手法が複数の研究者により考案されたことで,その後,圧倒的にこの方法が用いられるようになる.以下では,その手法の基礎となる考え方をBirdの論法(参考文献14)を用いて記述する.
いま,体積 $V_{cell}$のセルの中に$N$個の分子が存在すると考える.分子ペアの組合せは$N(N-1)/2$である.ある分子ペアの相対速度を$c_r$,衝突断面積を$\sigma_T$とすると,分子が$\Delta t$時間に物理空間を掃き清める体積は$\sigma_T c_r \Delta t$なので,この体積中に相手分子が存在すれば衝突がおきる.実際には体積$V_{cell}$の中にその分子が存在するのだから,この分子ペアが衝突する確率$P$は
\begin{equation}P=\frac{\sigma_T c_r \Delta t}{V_{cell}}\end{equation}
である.したがって通常の方法としては,$N(N-1)/2$の全ての組合せについて,それぞれのペアの衝突確率 $\sigma_T c_r \Delta t/V_{cell}$ を用いて衝突可否を検査し,衝突可と判定したものについてのみ衝突計算を実行する.さて,確率が1を超えては都合が悪いが,1を超えない範囲で,かつ,なるべく1に近づくように確率 $\sigma_T c_r \Delta t/V_{cell}$ の値を増加させ,その代わり,$N(N-1)/2$の組合せを全て検査せずに,確率が増加した分を相殺するように$N(N-1)/2$の数を減らして,分子ペアの検査回数を間引くことが考えられる.式(33)において,$V_{cell}$を$(\sigma_T c_r)_{max} \Delta t$ に置換えても確率は1を超えない.ここで,$(\sigma_T c_r)_{max}$ は衝突断面積と相対速度の積の最大値である.よって,$V_{cell}$を$(\sigma_T c_r)_{max} \Delta t$ に置換し,かつ,検査回数$N(N-1)/2$を
\begin{equation}N_{coll}=\frac{N(N-1)}{2} \frac{(\sigma_T c_r)_{max} \Delta t}{V_{cell}}\end{equation}
に減少させる.すなわち,分子ペアの選択を,式(34)で示す回数だけ繰返すが,その分子ペアが実際に衝突するかどうかの判断は,
\begin{equation}\frac{\sigma_T c_r \Delta t}{(\sigma_T c_r)_{max} \Delta t}=\frac{\sigma_T c_r}{(\sigma_T c_r)_{max}}\end{equation}
の確率で判定する.このようにして,全ての組合せを試行せずに効率よく衝突の計算を行う方法が完成した.なおこの方法では,$(\sigma_T c_r)_{max}$をあらかじめ見積もっておく必要がある.流れ場の状況にもよるが,通常は,$c_{r,max}$を $c_r$ の3倍程度にとり,それを用いて$(\sigma_T c_r)_{max}$の値を求める.
例題においては,最大相対速度 VRMAX は,平均相対速度の3倍 (CMUL$=3$) に設定する(154行).$(\sigma_T c_r)_{max}$は SMAX(156~158行)で表されている.なお,式(17)から明らかなように,$c_r$ に関する部分 $(c_{r,max})^{2(1-\omega)}$ だけを抜き出したものが SIG で,それ以外の部分が SIG2 である.さて,例題プログラムにおける分子間衝突の部分は,まだ,かなり先に位置するので,衝突計算プログラムの具体的説明は後回しにする.
これ以外の分子間衝突計算法として特筆すべきものに南部の方法(南部法,修正南部法)(参考文献20)がある.これは,ボルツマン方程式を忠実に衝突計算に組み入れた手法として高い評価を受けている.ただし,衝突時に片方の分子の速度だけしか変化させないので,計算速度が若干遅く,また,結果に含まれる統計的変動が他の手法よりも大きく現れるといった報告もあり,最大衝突数法に比べると利用される頻度は少ない.
式(35)の確率にしたがって衝突可と判定された分子ペアについては,VHS分子ならば式(20)~式(24)を,VSS分子ならば式(27)~式(32)を使って衝突後の相対速度の各成分 $c^*_{ri}$ $(i=1~3)$ が計算される.一方,質量中心速度の各成分 $c_{mi}$ $(i=1~3)$ は衝突前後で変化しないので,衝突前の速度を使って次式で計算される.
\begin{equation}
c_{mi}=\frac {m_1 c_{1i}+m_2 c_{2i}} {m_1+m_2}
\end{equation}
ここで,添え字1と2によって二つの分子を区別している.最終的に,二つの分子の速度成分 $(i=1~3)$ は以下の式で求められる.
\begin{equation}
c^*_{1i}=c_{mi}+\frac{m_2}{m_1+m_2} c^*_{ri}
\end{equation} \begin{equation}
c^*_{2i}=c_{mi}-\frac{m_1}{m_1+m_2} c^*_{ri}
\end{equation}
二原子分子あるいは多原子分子は,並進運動(並進エネルギモード)以外に,質量中心まわりの回転運動でもエネルギを蓄える(回転エネルギモード).また,高温になると振動運動も励起するようになる(振動エネルギモード).これをDSMC法で取り扱うのに,現時点では Larsen-Borgnakke の現象論的分子モデル(LBモデル)(参考文献21)がよく使われている.これは,全エネルギの保存を前提として,各エネルギモードの値を,平衡状態のエネルギ分布に基づいて算出するものである.ただし,この現象論的モデルを使うためには,例えば,並進モードと回転モードが平衡に至るための衝突数(あるいは弾性衝突と非弾性衝突の割合)をあらかじめ定めておく必要がある.
13.流入境界からの分子の流入
静止平衡にある気体では,単位時間,単位面積に入射する分子数は $n\overline{c}/4$ である.ここで,$\overline{c}$は平均分子速度である.もし気体が,面の法線に対し角$\theta$の方向からその面に向かって流速$C$で動いているならば,その入射分子数$N_{in}$は次式で求められる.
\begin{equation}
N_{in}=(1/4)n\overline{c} \ [\exp(-s^2\cos^2\theta)+\sqrt{\pi}s\cos\theta{\{1+\rm erf}(s\cos\theta)\}]
\end{equation}
ここで $s=C/c_{max}’$ で,erf は誤差関数である.もし $\theta=0$ ならば,
\begin{equation}N_{in}=(1/4)n\overline{c} \ [\exp(-s^2)+\sqrt{\pi}s\{1+{\rm erf}(s)\}]\end{equation}
となる.境界から流入する分子の数はこれらの式から求める.次に,流入分子の速度成分については,境界に平行な成分と垂直な成分に分けて考える.境界に平行な速度成分は,まず,平衡状態の分子の速度発生と同じ式(8)(10)(12)を用いて求め,それにその方向の巨視的流速を加えて完成する.一方,境界に垂直な分子速度成分を$u$とすると,$u$が大きい分子ほどそれに比例して多く流入するので,その分布関数は,平衡状態の分布関数$f_u$に$u$を掛算したものとなる.境界に垂直な流速を$U$とすると次のようになる.
\begin{equation}
uf_u=\frac{\beta}{\sqrt{\pi}}u\exp\{-\beta^2 (u-U)^2\}
\end{equation}
この分布から分子速度を発生するために棄却法を用いる.棄却法の場合,まず「考慮の対象とすべき$u$の範囲」を決め,さらに「分布関数の最大値」を求める必要がある.$u$の範囲としては,$U$が音速程度なら,$0\leq u \leq (3/\beta +U) \approx 4/\beta=4 c_{max}’$ で十分である.分布関数の最大値は,式(41)を$u$で微分してゼロとおけば求められる.すなわち,最大確率となる速度は次式となる.
\begin{equation}u_{m}=\frac{U+\sqrt{U^2+2/\beta^2}}{2}=\frac{U+\sqrt{U^2+4RT}}{2}\end{equation}
これを式(41)の$u$に代入すれば最大値$(uf_u)_{max}$が得られる.次に,具体的な棄却法の手順[1]~[3]を示す.
[1]一様乱数$R_{f1}$を求め,$u=(3/\beta +U)\times R_{f1}$ として,仮の速度$u$を求める.
[2]上記の$u$を式(41)に代入して$uf_u$を計算する.
[3]一様乱数$R_{f2}$を求め,もし $R_{f2}\leq uf_u/(uf_u)_{max}$ ならば $u$ を採用する.もし $R_{f2}>{uf_u/(uf_u)_{max}}$ ならば再び[1]の手順に戻り,$u$が採用されるまで[1]~[3]を繰り返す.
なお,式(41)における $\beta/\sqrt{\pi}$ は,手順[3]での $uf_u/(uf_u)_{max}$ の計算において分母分子に共通な係数なので省略できる.
さて,$U=0$の場合は,棄却法に依らずに速度成分$u$を求めることができる.その場合の分布関数は,式(41)の$U$をゼロとして次のように変形できる.
\begin{equation}uf_udu=\frac{\beta}{\sqrt{\pi}}u\exp(-\beta^2u^2)du=\frac{1}{2\sqrt{\pi}\beta}\exp(-\beta^2 u^2) d(\beta^2 u^2)\end{equation}
$\beta^2u^2$の範囲が$0\sim\infty$であることを考慮し,この分布関数を正規化して逆変換法を用いる.すなわち,累積分布関数を求め,これを一様乱数$R_f$に等しいとおく.
\begin{equation}F_{\beta^2u^2}=1-\exp(-\beta^2u^2)=R_f\end{equation}
式(11)のときと同様に,$1-R_f$と$R_f$は同値なので,
\begin{equation}\exp(-\beta^2u^2)=R_f\end{equation}
したがって,
\begin{equation}u=\frac{\sqrt{-\log_e R_f}}{\beta}=\sqrt{-2RT\log_e R_f}\end{equation}
なお,壁面で拡散反射した分子の垂直速度成分も同じように式(46)で求められる.ただし,そのときの$\beta$は壁面温度に相当する値である.
先に述べたように,例題におけるオリフィス入口の状態は,気体がよどみ点から等エントロピ変化でオリフィス入口に到達し,そこで流速が音速$(M=1)$になったものとして求める.TEX はオリフィス入口における気体温度,VTEX は最確速度,BETB はそれの逆数,EXX は音速,DEN01 は,よどみ点密度に対する比で表した密度である.168~170行で,UUM は,式(42)により速度$u_m$を求めたもの,UU は,式(41)から$\beta/\sqrt{\pi}$を除いたものである.174行の FIN0 は,式(40)によりオリフィスから流入する分子数を求めたもの,176行の DFIN0 は,下流境界からの流入分子数を求めたものである.また,FINB は,よどみ点における入射分子数である.ただし,いずれも単位面積,単位時間あたりの実分子数である.ES は,中心軸に平行な下流境界線の長さ(周囲境界の長さ)で,EO は中心軸に垂直な下流境界線長さ(円形境界面の半径長)である.
DTM は,分子移動と分子間衝突を分離する時間ステップ$\Delta t$で,小さくとるほどよいが,平均的速度の分子が $5\Delta t$ 程度の時間をかけてセルを横切るようにとれば十分である.もしセル長を平均自由行程と同程度とすると,$\Delta t$は,平均自由時間$\tau$(TAU)の1/5となる.しかし本例題では,オリフィス直後のセルの一辺長を,平均自由行程の約20倍にとっているので,$\Delta t=4\tau$とすれば釣合いがとれる.今回は計算を速くするために更に2倍にして,結局,$\tau$ の8倍としている(76行 ACT =8).
FIN は,オリフィス入口から流入するシミュレーション上の分子数,DFIN は,中心軸に垂直な下流境界から流入するシミュレーション分子数,DFINS は,軸に平行な下流境界(周囲境界)から流入するシミュレーション分子数である.NM は,シミュレーション分子の総数で,それの初期値は,最初に流れ場に置かれる分子の数となる.また,NMM には分子数の最大値を記憶する.
196~201行では,「通過分子数」と「セルのサンプリング情報」の配列変数を初期化(ゼロ化)している.なお 199行で,$10^{-10}$ を代入しているのは,後の計算で分母がゼロになるのを防ぐためである.これと同じ初期化処理は586~591行でも行っている.203行の U0(M)=0. は,下流垂直境界での流速を最初ゼロに設定したものであるが,550~551行でその流速の推定値が計算され,それが367行で使用されることになる.
205~207行で,「シミュレーションの開始」か「データ処理」かを判断し,それぞれのルーチンに分岐する.
209~221行では,最初に流れ場に置かれる分子の位置座標$x, y$と速度成分$u, v, w$が,式(5)および式(8)(10)(12)から作り出される.
224行の DO 100 が主たる繰返しルーチン(分子移動等の4ルーチンとセル情報サンプリング)の始まりである.
225~229行で,10回のRUNごとにエラー情報等を出力する.232行の DO 24 は,分子移動,分子所属セル調査,分子並べ替え,分子間衝突の4ルーチンを含む繰返しの開始である(ただし今回のデータでは繰返しは1回).
235行の IN は,最初から流れ場の中にある分子が移動する場合には $-1$を与えるが,境界から分子を流入させるときには流入分子数を入れる.
239行から物理空間における分子移動が始まるが,その説明は次項14に後回しにして,先に,流入境界からの分子流入プログラム(307行~371行)を説明する.
309~327行が,オリフィス孔からの分子流入である.309~311行では,実数値である流入分子数を乱数によって整数化している.312行の SS(5) は,$\Delta t$時間に,よどみ点密度にある気体の分子が,オリフィス孔と同じ断面積に入射する数 FINBAS(190行)の累積である.これは,流量(無次元コンダクタンス)を計算するための基準値として用いる.313行は,実際にオリフィス孔を通過する分子数のカウントである.315行で,流れ場内の分子数を1つ増加し,316行で$x$座標を,317行では,式(5)により$y$座標を求める.ただし,オリフィス半径よりも僅かに内側に収めている.319, 320, 326, 327行で,式(8)(10)(12)を用いて孔断面に平行な速度成分を計算し,321~325行において,式(41)と棄却法を用いて,孔に垂直な速度成分を計算している.
336~349行が,中心軸に平行な下流境界(周囲境界)からの分子流入,356~371行が,軸に垂直な下流境界からの分子流入である.境界に垂直な速度成分が$y$方向か$x$方向かの違いを除いてほとんど同じ計算処理となっている.339行は,下流境界から流入する分子数のカウントである.342行で,分子の$x$座標を 0~ES の間で一様に決めている.$y$座標は EO で一定である.345から348行で,境界に水平な速度成分を,349行では,式(46)を用いて垂直成分を計算している.ただし,垂直成分は負となることに注意する必要がある.少し先に進んで,363行は,式(5)を用いて分子の出発座標を計算している.なお,以前述べた境界付近で生ずるひずみを減ずるための処理をここに追加している.すなわち,垂直境界の流速をゼロにするのではなく,境界近傍の3つのセルの流速を平均して,垂直境界での流速 U0(N2) を推定し(547~552行),その値を 367行で U0(KU) として加算している.
<課題>367行における U0(KU) の加算を取り除いたプログラムで計算を行い,垂直境界付近のひずみの大きさを比較してみよ.
14.分子の物理空間(流れ場)内の移動
各々の分子は,その速度に応じて$\Delta t$時間だけ,他の分子とは独立に物理空間を移動する.その際,固体境界壁に衝突すれば,分子と壁との間で,運動量とエネルギの交換が行われ,分子軌跡は曲げられる.流れ場が複雑な境界壁形状をもっていると,分子は,その全ての境界壁に対してたえず衝突の可能性を考慮しながら移動しなければならない.また,壁面衝突の計算には,計算誤差の問題が常につきまとう.もし,分子が壁面を越えて移動したのに,計算誤差のため未だ衝突していないと判断されると,次の段階では分子が壁の中を突き進むことになり,シミュレーション全体に大きな問題を引き起こす可能性もある.DSMC法で,ほとんどの変数に倍精度を用いるのはこの計算誤差を極力さけるためである.本例題のように,大型配列に限って単精度を用いた場合には,分子移動ルーチンの最初で,それらを倍精度変数に置換え,移動計算を終了した後に,データを再び単精度配列に戻すという処理を行うとよい.
以上のように,DSMC法で新たにプログラムを作る場合,通常,ほとんどの労力が,この分子移動ルーチンの作成に充てられる.
分子と壁との衝突は,一般に,分子軌跡の方程式と壁面方程式を連立させて解くことにより求める.例えば,二次元空間に次式
\begin{equation}y=ax+b\end{equation}
で表現できる壁面があったとする.分子の速度が$u, v$ で,初期座標が$x_0, y_0$ ならば,時間を$t$としたときの分子軌跡の方程式は
\begin{equation}x=x_0+ut, \ y=y_0+vt\end{equation}
となる.したがって,分子が壁に衝突するまでの時間$t$は,式(47)と式(48)を連立させて次のように求められる.
\begin{equation}t=\frac{ax_0-y_0+b}{v-au}\end{equation}
$t$が負であったり,分子が移動できる時間$\Delta t_r$を超えていたら,分子は壁に衝突できない.また,たとえ$t$が条件を満足していても,この$t$を式(48)に代入して衝突する位置を求め,それが計算領域から外れていた場合にもやはり衝突はない.
なお,壁面方程式が $x=0$ の場合の衝突時間は以下のようになる.
\begin{equation}t=-x_0/u\end{equation}
次に,簡単な壁面方程式について,衝突時刻を求める式を紹介する.
[1]円($x^2+y^2=r^2$)の内側を分子が移動する場合
\begin{equation}t=\frac{-(ux_0+vy_0)+\sqrt{(ux_0+vy_0)^2-(u^2+v^2)(x_0^2+y_0^2-r^2)}}{u^2+v^2}\end{equation}
むろん,$t$が分子の移動可能時間$\Delta t_r$を超えていたら衝突はない.
[2]円($x^2+y^2=r^2$)の外側を分子が移動する場合
\begin{equation}t=\frac{-(ux_0+vy_0)-\sqrt{(ux_0+vy_0)^2-(u^2+v^2)(x_0^2+y_0^2-r^2)}}{u^2+v^2}\end{equation}
この場合も,$t$が分子の移動可能時間$\Delta t_r$を超えていたら衝突はない.また,平方根の中が負の場合,あるいは,解が負の場合も衝突はない.
[3]上記[1][2]の二つの円で作られる二重円内空間で分子が移動する場合には,先に内円との衝突を調べる.内円と衝突しない場合に,外円との衝突の有無を調査する.なお,外円には二度以上続けて衝突する可能性があることに注意する必要がある.
[4]球($x^2+y^2+z^2=r^2$)の内側を分子が移動する場合
\begin{equation}t=\frac{-B+\sqrt{B^2-AC}}{A}, \ \ A=u^2+v^2+w^2\end{equation} \begin{equation}B=ux_0+vy_0+wz_0, \ \ C=x_0^2+y_0^2+z_0^2-r^2\end{equation}
[5]球($x^2+y^2+z^2=r^2$)の外側を分子が移動する場合
\begin{equation}t=\frac{-B-\sqrt{B^2-AC}}{A}, \ \ A=u^2+v^2+w^2\end{equation} \begin{equation}B=ux_0+vy_0+wz_0, \ \ C=x_0^2+y_0^2+z_0^2-r^2\end{equation}
[6]上記[4][5]の二つの球で作られる二重球内空間で分子が移動する場合には,先に内球との衝突を調べる.内球と衝突しない場合に,外球との衝突の有無を調査する.
<課題>円錐表面の内部あるいは外部を分子が移動する場合の衝突時刻を求めよ.
軸対称空間における分子移動では,移動後,座標回転の操作を行う必要がある.分子は三つの速度成分に応じて空間移動を行うが,位置座標は二つしか保持されないので,残りの一つの座標を絶えずゼロにするような処理が必要である.いま,軸に垂直に $y$-$z$ 平面を考える.移動前の座標を $(y_0, 0)$,速度を $(v_0, w_0)$ とすると,時間$\Delta t$後の新しい座標 $y$ と速度成分 $v, w$ は,回転操作によって次式のようになる.
\begin{equation}y=\sqrt{(y_0+v_0\Delta t)^2+(w_0\Delta t)^2}\end{equation}\begin{equation}v=\{v_0(y_0+v_0\Delta t)+w_0^2\Delta t\}/y\end{equation}\begin{equation}w=w_0y_0/y\end{equation}
移動の途中で分子が壁面に衝突した場合,通常の壁面(工学壁面)では,拡散反射(散乱反射)の計算を行う.拡散反射とは,入射時に分子の持っていた運動量とエネルギは全て壁に吸収され,分子は壁に完全になじんだものとして,新しい反射速度が,壁の温度における平衡状態分布から算出されるものである.すなわち,まず,その壁面に衝突するまでの時間を求めて,全移動時間から差引き,反射後の飛行時間を求める.次に,以下のように反射後の速度成分を求めて,その新しい速度で分子を飛行させる.
いま,二次元空間において壁面の法線ベクトルが$x$軸から角度$\phi$だけ傾いているものとする(図3参照).
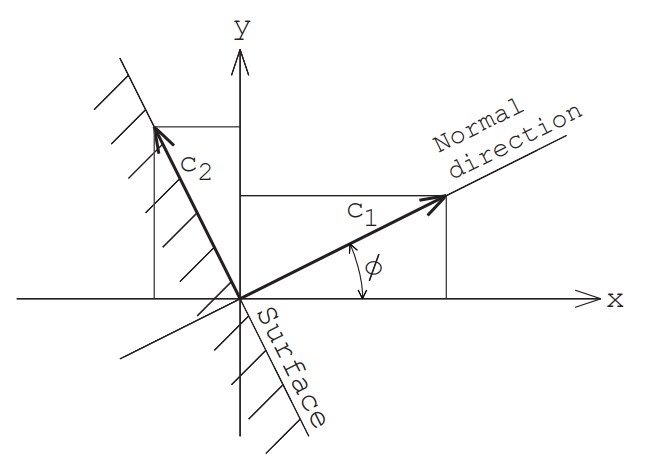
まず壁面に垂直な方向の速度成分 $c_1$ と水平方向の速度成分二つ $c_2, \ c_3$ を求める.これらは,巨視的速度ゼロで境界から流入する分子の速度成分の発生と同じ式で計算できる.
\begin{equation}c_1=\sqrt{-2RT_w\log_e R_{f1}}\end{equation} \begin{equation}\theta=2\pi R_{f2}\end{equation} \begin{equation}r=\sqrt{-2RT_w\log_e R_{f3}}\end{equation} \begin{equation}c_2=r \sin \theta, \ c_3=r \cos \theta\end{equation}
ここで,$T_w$ は壁面温度である.
次に,これらの速度を以下のように $x, y, z$ 方向の速度成分 $u, v, w$ に変換する.
\begin{equation}u=c_1 \cos\phi -c_2 \sin\phi\end{equation} \begin{equation}v=c_1 \sin\phi +c_2 \cos\phi\end{equation} \begin{equation}w=c_3\end{equation}
壁面反射として考えられるもう一つのものは,鏡面反射である.入射角と反射角が等しく,壁に垂直な速度成分が反転する以外は分子速度に変化がなく,分子と壁との間にエネルギのやりとりはない.一般には,このような面は存在しないが,対称面を考えた場合にこの反射となる.なお,拡散反射と鏡面反射の割合(適応係数)をあらかじめ定めて,その値に応じて両者の中間的な反射を模擬する方法もある.この方法には,一回の反射を乱数により拡散反射か鏡面反射のどちらかに決める方法と,一回の反射における速度成分を,拡散反射と鏡面反射の両者から合成する方法とが考えられる.前者が一般的であるが,後者の方法では,一つの入射角度でも木の葉状(lobular)の反射分布を簡単に実現できるという利点がある.
本来,反射分子の出発点としては,壁面上の点をとるべきであるが,その場合,計算誤差によって壁面内部からの出発となる可能性があり,シミュレーションに悪影響を及ぼすことがある.これを防ぐためには,壁面から少し浮かした点(流れ場へ少し入り込んだ位置)から分子を飛行させるのがよい.どの程度浮かせるかは,壁面の形状によって異なるが,セル長の$1/1000\sim 1/100$ 程度が無難であろう.ただし,壁が凹面形状である場合,あるいは,壁面方程式が複雑で出発点の計算に誤差が出やすい場合には,さらに大きく浮かせる必要がある.
239行からが分子移動のルーチンである.分子番号を一つ進めた後,計算誤差を少なくするために,単精度配列に記憶されている位置座標と速度成分を,いったん倍精度変数に置き換える.さて,最初から流れ場に存在していた分子については,時間ステップ$\Delta t$をそのまま移動時間に充てるが,境界から新しく流入した分子には,$\Delta t$の乱数倍を与える(245~249行).すなわち,分子が流入境界を通過する前にすでに時間を費やしていることを考慮した処置である.これを怠ると,境界付近にひずみが生じる.250行で,まず分子を無条件に$\Delta t$だけ移動させる.252~271行のIFブロックの中は,分子の移動先の$x$座標が負になったときの処理である.まず,253~256行で,式(50)により分子が$x=0$に達する時刻を求め,さらに式(57)からそのときの$y$座標を求める.この$y$座標がオリフィス半径より小さければ分子はオリフィス孔を逆流したことになるので,281行でそれをカウントした後,その分子を計算領域から捨去る処理(284~290行)をする.また,$y$座標が,流れ場の$y$方向境界 EO よりも大きい場合には,オリフィス壁に衝突する以前に計算領域から飛び出していたことになるので,283行でそれをカウントし,やはり分子捨去り処理に移る.上記二つのIF文のいずれにも該当しない分子は,259~270行で,壁面での反射処理が行われる.259, 260行で,式(58)(59)により壁面に衝突する直前の分子速度$v, w$を求めているが,この二行は本計算に直接必要ないものである.しかし,分子と壁面との間で交換される運動量とエネルギの収支を求める場合,あるいは,反射の一部に鏡面反射の性格を組み込む場合に必要となるので,あえてプログラムに書き込んである.261行で反射後に移動できる時間を求めた後,263~267行で,式(60)~(63)により反射後の速度成分を計算している.なお,オリフィス壁面の法線ベクトルは$x$軸と一致するので,式(64)~(66)は必要ない.268, 269行では,分子の出発点の座標を決めている.前述したように,$x$座標は,セル長の$1/1000$だけオリフィス面より浮かせて与えている.そして,270行で新たな移動先の$x$座標を求める.
オリフィス壁面に衝突しない分子,あるいは,壁面から新たに出発した分子の処理は,272~279行で行われる.272行で,流れ場の$x$方向境界 ES を超えた分子は,流出カウンタを進めた後,分子捨去り処理に移る.その境界を越えていない分子は,273~275行で,式(57)により移動後の$y$座標を計算する.その$y$座標を用いて,276行で,$y$方向境界を越えていないかどうかを調査する.境界を越えた分子は,やはり流出カウンタを進めて,分子捨去り処理に移る.上記二つのIF文に該当しない分子は,そのまま流れ場にとどまることになるので,式(58)(59)により移動後の速度成分$v, w$を求めた後,293~297行で,位置座標と速度成分の値を,倍精度変数から単精度配列に戻す.299行において,全ての分子の移動計算がまだ終っていなければ,次の分子の移動処理に移る.
ここで,分子捨去り処理を説明しておく.計算領域から飛び出た分子の情報は必要ないため,情報を記憶している配列から捨去ることになるが,その分子情報は配列内にランダムに記憶されている.したがって,ただ捨去るだけでは配列が虫食い状態になる.すなわち,新たに流入する分子の情報を記憶するために,配列内を整理しておく必要がある.そこで,284~290行に示すように,その時点で配列の最後尾に記憶されている情報を,捨去る分子情報が記憶されていた要素に移し変え,配列最後尾の番号(全分子数)を一つ減らす操作をするのである.
300~303行において,最初から流れ場にいた分子の移動計算が全て終わった後に,境界から流入する分子の移動計算を始める処理に移るが,その移動計算も終わったなら,最大分子数の更新を調査した後,次に「分子がどのセルに入っているかを求める計算」のルーチンに移る.
<課題>例題プログラムの「分子の空間移動ルーチン」について,流れ図を描き,分子の運動を追跡せよ.
15.分子の所属セル算出と参照配列上での分子の並べ替え
分子間衝突の計算に入る前に,それの準備としての手続きが必要である.分子の空間移動によって位置座標が変化するので,まず,各分子がどのセルに属するかを調査する.例題では,392~394行において,分子が属するセルの$x$方向の並び番号を式(13)により求める.ただし,式(13)の1の代わりに0.999999を用いて,値を低めに誘導して整数化し,セル番号がゼロになったら1に変える操作をする.これは計算誤差対策である.
一方,$y$方向は,まず等分割セルとして単純に,割算でセルの並び番号を求めるが,先に述べたように.中心軸に最も近い3つのセルは一つに結合しているので,その処理も含めて計算誤差対策を行っている(396~401行).403行で,$x$と$y$の二方向のセルの並び番号を用いて,全領域で一連に付けられたセル番号を定めている.なお,この計算の過程で,はぐれ分子(エラー分子)の調査を行うとよい.すなわち,計算誤差によって,わずかな確率ながら分子が壁内部へ侵入することが生じるし,あるいは,計算領域の外へ飛び出したはずの分子が何らかの理由でまだ生き残っている場合もある.この分子をそのままに放置すると,シミュレーション全体に致命的エラーを引き起こす可能性がある.そこで,それら分子をこの時点で調査し,エラー分子の数をカウントすると同時に適切な処理を施すものである.383~390行および404~407行がそれに相当する.
なお,エラーカウンタをたえず監視する(モニターに出力する)ことによって,プログラムのバグの調査もあわせて行う(エラーの回数が異常に多い場合はプログラムに誤りのあることが考えられる).例題では,227行でそれを行っている.
さて,分子間衝突の計算を容易にするため,参照用配列(Cross-referencing Array) LCR(K) 上で,分子を,それの属するセルの順に並べ直す処理が必要である.図4は,その処理によって作られる配列の例を示したもので,K が座席番号(番地)を意味し,LCR(K) に分子番号(分子識別番号)が記憶される.図4では,第1セルの分子数は6で,1番から6番までの6個の座席を確保し,先頭座席の一つ前の座席番号は0である.同様に,第2セルは,分子数が7で,7番から13番までの7個の座席を持ち,先頭座席の直前の番号は6,第3セルは,分子数5,14番から18番までの座席を持ち,先頭座席の直前は13番である.

この参照配列を作るために,まず最初,全てのセルについてセル内分子数を調べる.すなわち,414~418行において,セル内分子数 IC1(N) を全てゼロにした後,全ての分子についてその所属セルを調べながらセルの分子数をカウントしていく.次いで,419~423行で,セルの順にセル内分子数を累積していくことにより,LCR(K) 配列上の各セルの先頭位置を調べる.実際には,各セルの先頭位置より一つ前の番号(先頭座席$-1$)が IC2(N) の中に記憶される.その際,セル内分子数 IC1(N) は再びゼロにクリアされる.最後に,424~428行で,全ての分子について,所属セルの分子数をカウントしながら,IC2(N) を利用して参照配列上の座席にその分子番号を順に埋めていく.さて,この参照配列を利用する例として,分子間衝突の第一段階で,対象とするセルから任意に分子を選択する場合を考えてみる.セルに与えられた連続した座席番号の中から,ランダムに一つを定めれば,この配列を用いて分子番号が参照できるので,結果として,衝突に関与する分子の速度成分を得ることができる.
16.分子間衝突のプログラム – 衝突計算その3
分子間衝突の計算は,全セルにおよぶDOループ(433~509行)の中で,セルごとに行われる.435行では,セルに二個以上の分子がない場合,そのセルでの衝突計算をスキップする処理を行う.436, 437行は,式(34)により,衝突分子ペア選択の試行回数(衝突検査回数)を求めている.先に述べたように,衝突断面積$\sigma_T$は,シミュレーション分子数が実分子数に比べて少なくなった分,大きくする必要があるので,重み係数 WEI を用いてその補正を行っている.438~440行は,実数値としての衝突数を,乱数を用いて整数化する操作である.このようにして得られた衝突検査回数 ICN だけ,衝突ペア検査の繰返しを行い,衝突可となった場合は実際に分子間衝突の計算も行う(442~507行).
444~447行は,セル内分子数 IC1(N) と [先頭座席ー1] IC2(N) および参照配列 LCR(K) を用いて,セル内にある分子の一つをランダムに選ぶ計算である.ここで,0.9999999の加算と小数点以下切捨て処理によって座席番号の低め誘導を行い,番号が小さ過ぎたら1を加算する.この操作は,以前にも説明した計算誤差対策である.447行で,参照配列により,座席番号を分子番号に変換している.同様に,449~453行が,もう一つの分子を選ぶ計算である.ただし,同じ分子を選ばないための処理が加えられている.455~459行では,二つの分子の相対速度が計算されている.461, 462行の RVRALL と RVRGT は,$(\sigma_T c_r)_{max}$の見積もりが妥当なものであるか否かを検査する変数で,RVRGT が RVRALL に比べて十分小さければ問題ない.226, 227行で,これの比 OV の途中経過を出力している.463行は,式(35)により,分子ペアの衝突確率を計算したものである.ただし,式(35)の分母分子に共通な部分は省略してある.465行において,一様乱数が衝突確率よりも小さいならば,この分子ペアは衝突することになり 467行以下が実行されるが,衝突確率より大きいなら次のペアの衝突検査に移る.
468~473行は,式(20)~(24)によって,VHS分子の衝突後の相対速度成分を計算したもので,475~492行は,式(26)(28)~(32)によって,VSS分子の衝突後の相対速度成分を計算したものである.495行は,衝突数をカウントしているもので本例題では直接は使用しない.497~505行は,式(36)~(38)により,衝突後の両分子の速度成分を算出するものである.ここで,VCCM は質量中心速度であるが,分子は同じ質量なので$m_1$と$m_2$はプログラムの中に現れない.
17.流れ場データのサンプリング
上述した分子移動と分子間衝突が限りなく繰り返され,流れ場が形作られていくが,計算機の中で変化するのは,多数の分子の位置座標と速度成分だけである.流れ場の情報として実際にほしいものは,密度(数密度),流れ速度,温度であるから,それを算出する必要がある.数密度については各セル内の分子数$N$
\begin{equation}N=\sum_{i=1}^{N}1\end{equation} とセル体積$V_{cell}$から求められる.また,流れ速度$U, V, W$は,セル内にある分子の速度を平均すれば得られる.
\begin{equation}U=\frac{1}{N}\sum_{i=1}^{N}u_{i}, \ \ V=\frac{1}{N}\sum_{i=1}^{N}v_{i}, \ \ W=\frac{1}{N}\sum_{i=1}^{N}w_{i}\end{equation} 単原子分子の場合,温度$T$は「気体分子の持つ並進エネルギ」から「流れ速度による運動エネルギ」を差し引いて計算できる(多原子分子の場合は,分子の回転および振動のエネルギも考慮する).例えば,$x$方向温度$T_x$は次のようになる.
\begin{equation}T_x=\{\frac{1}{N}\sum_{i=1}^{N}u_{i}^{2}-\bigl(\frac{1}{N}\sum_{i=1}^{N}u_{i}\bigl)^2\}/R \end{equation} $T_y$, $T_z$についても同様に求め,それらの平均として温度$T$が求められる.
\begin{equation}T=(T_x+T_y+T_z)/3\end{equation}
なお,圧力を求めたい場合は,状態方程式が成立するときは密度と温度から算出し,非平衡が強く状態方程式が使えないときは,圧力を求めたい位置に仮想壁を置き(プログラム上),そこを通過する分子の運動量から算出する.
例題において 514行から始まるDOループは,セル内情報のサンプリング処理である.個々の分子についてその所属セルを調べ,517行は式(67)で分子数をカウント,518~520行は,式(68)における$\sum u_i$と$\sum v_i$と$\sum w_i$の部分,521行は,式(69)における$\sum u_i^2$で,522, 523行は,$\sum v_i^2$ と $\sum w_i^2$である.なお,最終的な密度,速度,温度の値は,プログラムの最後にあるデータ処理ルーチンで計算される.
セル内サンプリングデータの途中集計は K100 回ごとにファイルに出力される.
529, 530行は,その回数に達したかどうかを判断するもので,K100 に達したら531~591行が実行され,まだその回数に達していなければ224行に戻る.
K100 回ごとに出力されるファイル名は毎回異なるものである.すなわち, ‘sjetc01’, ‘sjetc02’, …. のように名前づけられる.531~542行で,その名前を決定し,544~553行で,セル情報をファイルに出力している.
もう一つの出力ファイルは,オリフィス入口および下流境界における正味の通過分子数である.例題では,よどみ点における入射分子数$(1/4)n\overline{c}$で無次元化しており,556~561行でそれを行っている.556行の A は,通過分子数を実分子の数として表すための係数であるが,この例題では意味を持たない.なお,この無次元通過分子数は,下流圧力(今回は圧力比1/50)を無視するならば,無次元コンダクタンスになる.この出力ファイルは,毎回同じファイル名 ‘sjet4’ で出力されるが,「それまでに出力された個々のデータ」と「最新データからそれら個々のデータまで遡った平均値」をあわせて出力するようになっている.例題は,自由噴流の定常状態を計算するものであるが,DSMC法では,定常に達する前に必ず非定常状態を経験する.したがって,出力されるデータの何回目で定常に達したかを見積もる必要があるが,この通過分子数データを用いればそれができる.すなわち,最新データから遡って求めた平均値が安定していれば,そこでは,ほぼ定常に達していると言える.さらに厳密に行うとすれば,$t$ 分布表を用いた統計計算により,平均値からの誤差範囲も考慮して決定するのがよい.563~584行において,その平均化操作を行った上で,ファイル出力を行っている.586~591行は,配列変数 SS と SC の初期化(ゼロ化)処理である.
18.最終データ処理
例題プログラムでは,最終データ処理のルーチンが,メインルーチンと切り離して作られている.すなわち,いったんシミュレーションを終えたら,上述の要領で,何回目の出力データ以降を平均するのかを決め,再び,プログラムを実行する.205~207行において,’2′ を入力すれば,データ処理ルーチンに移る.601行の XLIM は,流れ場の$x$方向について,オリフィス径の何倍の位置まで処理するかを入力するものである.例題の下流境界は,無限遠下流の状態を境界条件としているので,特に,中心軸に垂直な下流境界の近傍では結果にひずみの出る可能性がある.そこで,境界近傍のデータを切り捨てるために,例えば今回の計算では,余裕をもって ’10’ 程度の値を入力する(ひずみの程度を知りたければ ’16’ を入力する).次の入力データ KDO1 と KDO2 は,処理データの開始番号と終了番号である.今回の計算では,6回目以降は定常状態に達していると考えられるので ‘6’ と ’20’ を入れる.もちろん,開始と終了の番号を共に,例えば ‘1’ を入力し,非定常状態を観測することもできる.ただし,相当長い時間を平均した非定常結果なので,厳密な意味の非定常状態ではない.607~634行において,複数のファイルからセル情報を読み込み,平均化処理をしている.
636~671行が,最終的な流れ場データを計算し,ファイル ‘OUTD’ に出力するルーチンである.DO 302の制御変数 I は,$y$方向のセルの並びの順に変化し,DO 303の制御変数 J は,$x$方向のセルの並びの順に変化する.639~643行で,セル中心の$y$座標を求めている.中心軸に最も近い三つのセルは結合されているのでこのような計算となる.646~648行は,セル中心の$x$座標を求めている.649, 650行は,セルの中心座標をオリフィス直径で無次元化したもので,651行は,$x$座標がデータ処理打切り位置を超えた場合の処理である.652~654行は,よどみ点密度を1として各セルの密度を表現したものである(よどみ点密度による無次元化).655~657行は,式(68)で流れの速度を計算したもの,658~660行は,式(69)で各方向の温度を計算したものである.661行は,式(70)で平均温度を計算したもの,662行は,中心軸に垂直な温度の平均である.663, 664行では,流れ速度を音速$\sqrt{\gamma R T}$ で割算してマッハ数を求めている($\gamma$は比熱比).
なお665, 666行でファイルに出力する際,速度については,よどみ点の最確速度$c_{max}’$で無次元化し,温度については,よどみ点温度で無次元化している.
出力データの並びは,各セルについて,$x$座標,$y$座標,密度,$x$方向速度,$y$方向速度,平均温度,軸に平行な温度,軸に垂直な温度,マッハ数の順である.パラメトリックなデータに配列されており,フリーのソフトウェア gnuplot を使って三次元グラフ(鳥瞰図)が直接描けるようになっている.
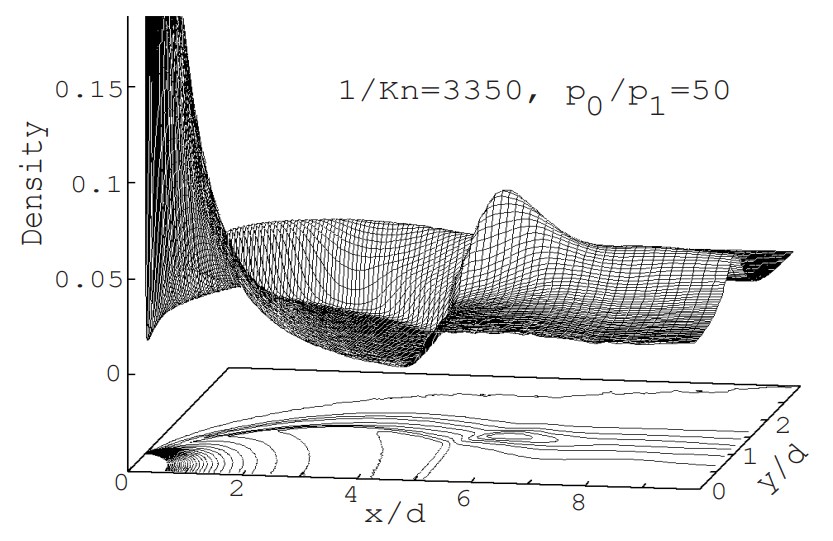
図5は,例題で計算された結果を gnuplot(v3.5) で処理した密度分布である.高さ方向に拡大してあるので,マッハディスクもバレルショクもはっきりと観測できる.ただし,例題では,オリフィスより上流に計算領域を設けていないため流量が実際より大きくなり,噴流自体が大きくなって,マッハディスクも本来の位置より下流側にずれている.
<課題>噴流形成における背圧の影響について考えたとき,流れ場の条件によっては,噴流軸に平行な下流境界(周囲境界)の影響が支配的で,噴流軸に垂直な下流境界は殆ど影響を及ぼさないことがある.例題プログラムで,噴流軸に垂直な下流境界だけを完全真空と設定して計算を行い,結果を比較してみよ.
19.例題プログラムからの発展
良いプログラムを作るこつは,自らが多くのプログラムを作成することである.この例題プログラムを基礎にして,さらに複雑な問題に挑戦されることを望むものである.最後に,いくつかの発展課題を付記する.
[1]例題では,オリフィスより上流側に計算領域を持たないため自由噴流が大きくなり,また,オリフィス出口直後の噴流形状が実際とは少し異なるものになっている.そこで,上流側に計算領域を持つプログラムを作りDSMC計算を行ってみよ.その際,上流境界における境界条件はどのように与えたらよいか.
[2]オリフィスに厚みを設けてみよ.また,円錐ノズルにするにはどうしたらよいか.
[3]例題では,セルの長さを場所に応じて変化させている.もし,時間ステップも場所に応じて変化させられれば,圧力比が大きな状況で,効率のよい計算が可能になる.これをどのように実現したらよいか(難問).
[4]例題は軸対称の流れ場であるが,三次元流れ場にできれば,矩形のオリフィスを通る自由噴流も計算できる.例題プログラムをどのように変更したらよいか.
[5]混合気体の流れを実現するためには,例題プログラムのどこを変更すればよいか.
例題プログラムを参照するには,ここをクリックしてください(プログラム各行の左側の1桁~3桁の数字とそれに続く空白1つは,行番号(1~677)を示したもので,プログラムには含まれないことに注意).